发布时间:2023-08-28 16:53:55
序言:写作是分享个人见解和探索未知领域的桥梁,我们为您精选了8篇的数学与基础数学样本,期待这些样本能够为您提供丰富的参考和启发,请尽情阅读。
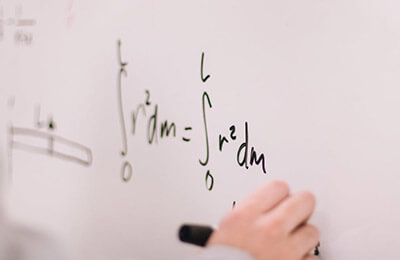
(1.大连海事大学智能科学与技术系,辽宁大连116000:
2.国网辽宁省电力有限公司大连供电公司,辽宁大连116000)
摘要:结合fMRI数据处理方法,介绍相关的数学基础,阐述如何完成认知实验及数据处理,实现理论与实践相结合的教学方法。
关键词 :脑与认知科学;功能磁共振;数据分析方法;基础数学
基金项目:国家自然科学基金项目( 61472()58, 61173035);新世纪优秀人才计划(NCET-11-0861)。
第一作者简介:刘洪波,男,教授,研究方向为认知计算及大数据,thb@dlmu.edu.cn。
1 背景
脑与认知科学课程是智能科学与技术专业的主干课,涉及心理学、神经科学、计算机科学与技术等,学习这门课程不仅能启发智能系统设计模式,更有利于脑机接口、生物医学等方面的应用。在这门课程的教学过程中,容易忽略其中的数学基础。特别的,随着fMRI、EEG等无损影像技术的发展,如何利用其中的影像数据提取其中的丰富信息已成为人们关注的焦点,而其中的数学基础起到重要的作用。
fMRI成像是20世纪90年代初出现的研究工具,其原理是基于血氧水平依赖(blood oxygenation level dependent,BOLD)信号。由于大脑在活动期间,血流变化很小,在1.5T的磁场强度下,灰质发生的血液动力学信号变化通常为2%~5%,而且还受呼吸、心跳等生理活动的影响。因此,fMRI数据集是受到系统噪声影响的时间序列数据集。由于是观测型数据,这就需要借助合理数学的方式来进行处理,所以在脑与认知科学的课程中需要强化这方面的基础。
2 数学基础
2.1 相关分析
相关分析法是一种简单的用于分析脑功能连接的方法。它是通过计算基于感兴趣区(ROI)间的Pearson相关系数得到以ROI为节点的边的强度。当相关系数达到某一阈值时,就认为这两个脑区之间存在功能连接。
2.2 广义线性模型
Friston提出的统计学参数映射方法(statistical parametric mapping,SPM)6-8]是一种有效提取脑激活区且具有鲁棒性的方法。该方法本质上是利用广义线性模型( general linear model,GLM)克服系统误差。GLM的模型假设如式(2)所示。
式中:Y表示待分析的fMRI信号;X表示设计好的参考矩阵;β表示待估计的参数;ε表示误差。
β的估计根据度量准则的不同而不同。特别的,当度量准则为欧式距离时,β的无偏估计量可由式(3)完成对β的估计后,就可以利用t检验对得到的线性模型进行逐像素的分析,并以此给出大脑激活图像。
2.3 独立成分分析
独立成分分析( independent component anal-ysis,ICA)是一种无监督的学习方法。该方法首先由McKeown[9-10]应用于fMRI数据集中。ICA假设为观测信号是由源信号经过未知的线性规则叠加而成。考虑一个M维观测向量X= (x1,X2,…,XM)T,则ICA的模型假设可由式(4)表示。
X=AS (4)
式中:S=(s1,s2…,,SN)T表示N维源向量;A表示未知的线性混合矩阵,通常来说M≥N,且A为满秩。
独立成分的目的就是估计一个解混矩阵WN×M,使得由式(5)得到的Y接近真实源信号S。易见式(5)等价于式(4)。
Y= WX (5)
因此ICA又可以被归为优化问题,目前主要求解方法分为不动点(fix-point)算法和自适应。
ICA的自适应算法也称作基于梯度的自适应算法,可以通过优化判据对待估参数进行逐步优化,最终得到稳定的输出结果。其中一种优化判据是基于Infomax准则的优化判据,它可以写为
式中:gi(yi)表示一个合适的非线性函数;ri=gi(Yi);H(x)是输入信号的熵,它与W的选择无关与Informax等梯度算法相比,固定点算法对待独立成分的处理方式则不同。固定点算法一般分为两步:第一步先把每个观测分量Xk白化为Zk;第二步则寻求Zk的最优投影方向。
固定点算法首先由式(4)和式(5)可知,y= WAS=VS。若假定S=(S1,S2,…,SN)T的各分量同分布且为非高斯的,则根据中心极限定理可知,yj比每个si更加接近高斯分布。当且仅当yi=Sk,k={1,2,…,N}时,Yi的非高斯性最大。而衡量非高斯性的理想度量即负熵,负熵的定义如式(7)所示,由Edgeworth级数展开,得到由高阶统计量近似表示的形式(8)。其中Z的每个分量由X零均值切方差归一,即经过白化后的矩阵Z=(Z1,Z2…,ZN)T。k4为高阶统计量,
3 教学实践
上述介绍几种比较常用的基于fMRI的数据分析方法,这些方法不仅可以用于构建大脑功能网络,也可以用于考察脑激活与外界刺激的联系。其中,相关分析作为一种朴素的统计方法,由于fMRI自身信噪比不佳,若直接应用于fMRI信号分析,效果相对一般。但是一些配合小波分析等其他特征提取方法,依然可以取得相对理想的效果。目前主要用于静息态数据的分析,应用工具包包括rest、dparsf等。广义线性模型的应用则比较广泛,并且SPM自身的功能也比较完善,可以作为多种分析策略的特征提取手段。独立成分分析则是一种较新的分析方法,与前两个模型一样也有相应的软件实现,如GIFT、MICA等。其实验结果的生理学含义有待于进一步验证。
3.1 基于E-prime的脑与认知科学实验设计
E-Prime软件是由美国PST( PsychologySoftware Tools,Inc.)公司开发的一套针对心理与行为科学研究的实验设计、生成和运行软件,以其易学易用、计时精度高等特点在国内外心理学界得到了广泛应用,已经成为全球通用的标准化认知心理实验生成系统。在学生学习了脑与认知科学相关理论并具备基础的数据库相关知识之后向学生传授如何利用E-Prime软件编制脑与认知科学实验程序,具有很强的实践性。本实验以上机编程操作为主,首先练习利用E-Prime软件在GUI界面下开发一个脑与认知科学实验程序,然后练习如何利用E-Basic语言编写脚本实验程序以实现GUI环境下难以实现的部分实验功能,最后采用E-Prime软件行为数据分析模块练习行为数据的统计与分析。经过本实验的训练后,学生熟练地掌握了脑与认知科学实验设计的方法,更深入地领会脑与认知科学研究方法的底层逻辑。
实验目的在于训练学生利用E-Prime软件开发脑与科学实验程序,以提高其从事脑科学与认知科学领域研究的能力。实验教学中鼓励学生自主设计实验程序,以达到提高实验程序开发技巧、培养动手能力及科研能力的目的。此外,还要注意不断深化和扩展教学内容,注意向学生介绍近年来出现的新的实验范式及如何利用E-Prime编程实现,以加强本实验课对于学生以后从事脑科学与认知科学研究的实用性。
3.2 基于SPM的脑功能成像数据分析实验
SPM是由英国神经科学领域、统计领域、图像处理领域的科学家Friston等人在通用数学软件包Matlab上开发的软件系统,具有非常强大的统计功能。SPM指的是统计参数图像,也就是这个软件的最终输出。它对所有成像数据的每一个体素点都分别计算,得出包含有每个体素点参数值的图像,这个参数图像是许多单次扫描图像所包含信息的精简和压缩。目前SPM通用的版本为SPM8,以前的版本主要有SPM94、SPM96、PM99、SPM2和SPM5,它们在进行脑功能图像初步分析方面基本是一致的。SPM对脑功能成像数据的处理包括预处理、建模和统计推论三个步骤。
实验分为两步,首先让学生参加fMRI实验,每人完成一个简短的脑与认知实验程序并采集个人的功能成像数据,然后上机基于SPM系统分析自己的脑成像数据,最终获取个人在进行认知任务时大脑的激活示意图。经过本实验的训练后,学生掌握了脑功能成像数据分析处理的思路和方法,在成功获得了自己进行认知任务时大脑的活动模式后极大激发了他们对于脑科学与认知科学研究的兴趣。在教学过程中注意介绍基于脑功能成像技术的脑与认知科学研究的最新成果,以及脑功能成像技术的最新进展,实验中详细介绍SPM处理数据每一步的目的和原理,加强学生对于脑功能成像技术和功能数据分析处理的理解,从而提高其从事脑功能成像领域研究的能力。
3.3 基于Matlab的脑功能连通模式构建实验
Matlab是由美国Mathworks公司的主要面对科学计算、可视化以及交互式程序设计的高科技计算环境,它将数值分析、矩阵计算、科学数据可视化以及非线性动态系统的建模和仿真等诸多强大功能集成在一个易于使用的视窗环境中,为科学研究、工程设计以及必须进行有效数值计算的众多科学领域提供了一种全面的解决方案,并在很大程度上摆脱了传统非交互式程序设计语言(如C、Fortran)的编辑模式,在医学图像分析处理领域得到了广泛应用。实际上SPM系统就是基于Matlab平台的程序包,本实验不依赖SPM系统,基于预处理完成后的脑功能成像数据和Matlab编程平台,采用相关分析方法分析大脑激活区活动的关联模式。
当前的脑功能成像研究已经不像以前那样着重于脑区功能定位,即单纯确定哪些脑区参与了研究任务,现在大都从整体和动态角度研究任务过程中参与的脑区以及脑区间的反应模式和时空关系,并建立脑内信息加工的相关网络与模型。基于相关分析的功能连接分析是近期兴起的一种脑功能成像分析技术,即分析脑区间的相互作用和协同竞争的关系,在获得感兴趣区和脑激活图的基础上,进行了功能连接分析。实验首先对成像数据进行预处理,目的是尽可能地消除个体差异,并把所有被试的数据统一到一个标准下测量,预处理过程和SPM处理是一致的;其次基于SPM处理结果,确定大脑感兴趣区中t值最强点以及它所在的簇,所谓的簇是指以t值最强点为中心的27个体素;第三,根据体素点坐标位置提取信号值,即提取t值最强点所在的簇27个体素信号的平均值;第四,采用相关分析方法,感兴趣区信号值之间两两求相关系数,即得感兴趣区之间的有效性连接程度。
本实验对于Matlab编程基础要求较高,因此实验分段进行,先练习基础变量的设置和计算,然后练习几个主要函数(如fopen、fseek、fread和corrcoef等)的分析处理功能,最后整合成完整的程序。数据分析完成后,鼓励学生发挥想象力,构画脑功能连通模式图。通过本实验,学生掌握了Matlab处理脑功能成像数据的基本原理和方法,进一步加强了其在脑功能成像领域进行研究的能力。
4 结语
脑与认知科学课程中的数学基础强化与实践,在智能科学与技术专业课程体系中具有重要作用,学生需要这些知识作为专业基础,掌握其基本知识、基本理论、基本方法及基本技能,还需要注重思维能力的培养。但是对于以计算机科学为基础的智能科学与技术专业本科生来说,脑与认知科学有专业跨度,比较难掌握。发挥理工科的数学与计算优势,结合实验及数据处理、获取第一手的具体实践的教学方式方法值得我们去研究和探索。我们在数学基础、课程教学与实践及专业特色的基础上,阐述强化理论基础、实验创新教学实践相结合的观点;根据大连海事大学智能科学与技术专业2012级和2013级的教学实际,探索新的教学方法,不断提高教师自身的素质和专业能力,注重学生理论学习和实践能力的培养,为国家和社会培养出更多基础扎实的创新性人才。
参考文献:
[1] Logothetis N K. What we can do and what we cannot do with fMRI[J]. Nature, 2008, 453(7197): 869-878.
[2] Kwong K K, Belliveau J W, Chesler D A, et al. Dynamic magnet- ic resonance imaging of human brain activity during primary sensory stimulation[C]//Proceedings ofthe National Academy of sciences, 1992, 89(12): 5675-5679.
[3] Ogawa S, Tank D W, Menon R, et al. Intrinsic signal changes accom- panying sensory stimulation: functional brain mapping with magnetic resonance imaging[C]// Proceedings of the National Academy of Sciences, 1992, 89(13): 5951-5955.
[4] Frackowiak R S, Friston K J, Frith C D, et al. Human brain function[M]. Salt Lake City: Academic Press, 2004.
[5] Bell A J, Sejnowski T J. An information-maximization approach to blind separation and blind deconvolution[J]. Neural computation, 1995, 7(6): 1129-1159.
[6] Friston K J, Holmes A P, Worsley K J, et al. Statistical parametric maps in functional imaging: a general linear approach[J]. Human Brain Mapping, 1994, 2(4): 189-210.
[7] Friston K J, Ashburner J T, Kiebel S J, et al. Statistical parametric mapping: The analysis of functional brain images[M]. Salt Lake City: Academic Press, 2011, 14: 178-191.
[8] Friston K J, Fletcher P, Josephs O, et al. Event-related fMRI: charac- terizing di erential responses[J]. Neuroimage, 1998, 7(1): 30-40.
[9] McKeown M J, Makeig S, Brown G G, et al. Analysis of fMRI data by blind separation into independent spatial components[J]. Human Brain Mapping, 1997, 6(3): 160-188.
[10] McKeown M J, Sejnowski T J. Independent component analysis of fMRI data: examining the assumptions[J]. Human brain mapping, 1998, 6(5-6): 368-372.
[11] Hyv " arinen A, Oja E. A fast fixed-point algorithm for independent com- ponent analysis[J]. Neural computation, 1997, 9(7):1483-1492.
[12] Bingham E, Hyvrinen A. A fast fixed-point algorithm for independent component analysis of complex valued signals[J]. Neurocomputing, 2000, 10(1): 1-8.
摘 要:素质教育的不断深入发展使得人们越来越重视学科素养,传统的只注重知识传授的初中数学教育方式已经无法培养出21世纪真正所需的人才。因此,在实际的教学过程中,数学教师要注意优化自己的教法,使所有学生能够意识到自己的主体地位,开展主动的学习活动,提升自己的数学素养,为每个学生的未来发展打下坚实的基础。
关键词:初中;数学;学科素养;教学策略
数学学科素养是指初中生既有丰富的数学知识,又能在学习活动中掌握科学的学习方式,还能够对他们所习得的知识了解得更加深刻,学会举一反三,了解数学的意义。数学在人们的生产生活中占据着重要的地位,随着信息技术的普及与发展,数学在人们生活生产中的地位愈加重要,它对推动社会进步、科技发展等都有重要意义。除此之外,数学也是初中生学好物理、化学等学科的基础。因此,教师必须要改变“老师讲,学生听;老师问,学生答”的被动教学方法,培养初中生的数学学科素养,使其掌握在生活中运用数学知识的能力。下面,笔者从培养初中生的探究思维、指导学生掌握科学的学习方式、加深学生的情感认知三个方面,讨论教师如何培养初中生的数学学科素养。
一、培养初中生的探究思维
数学家华罗庚曾经说过:“科学的灵感,决不是坐等可以等来的。如果说,科学上的发现有什么偶然的机遇的话,那么这种‘偶然的机遇’只能给那些学有素养的人,给那些善于思考的人,给那些具有锲而不舍的精神的人,而不会给懒汉。”因此,在教学活动中,教师应注意培养学生的探究思维,使其学会主动思考,以数学家的思维方式来学习数学。这并不只是为了让初中生在未来进入数学研究领域工作,而是为了让初中生养成勤于思考、勤于动手、爱学好问的好习惯。在《圆的有关性质》一课中,我利用圆规在黑板上画了一个圆,并让学生观察画图过程,总结圆的定义,系统学习圆心、半径等知识。然后,我问学生:“除了圆上的点到圆心的距离是一致的,还有其他的点与圆心的距离一致吗?”有的学生想了想,说:“没有。”然后,我让他们再亲自动手,探究这个问题的结论是否正确。
二、掌握科学的学习方法
数学学科具有抽象性、思维性,要想学好数学,单纯依赖死记硬背是不行的,学生必须要掌握科学的学习方法,才能够灵活应对任何数学问题。由于很多教师的教学意识不够先进,他们还没有转变以中考为指向标的教学意识,从而过于重视初中生的数学成绩,反而忽视了培养初中生的数学思维,忽视了学习方法的重要性。这就导致很多学生只会做某道数学题,但凡这个题目往更深层次发展,或稍加变动,就会让初中生束手无策。尤其是初三学生直接面临中考,因此他们的学习时间非常紧张,学习任务很重,导致他们在学习数学的过程中感到十分压抑。因此,教师必须要把数学教学的基点放在如何培养初中生的学科素养上,使其掌握学习数学的科学方法,在提高他们数学知识与能力的同时,减轻他们的负担。在《点和圆、直线和圆的位置关系》一课中,我指导学生亲自动手,分小组探究点与圆的几种位置关系。每个学生都需要在小组内发言,将他们亲自动手测量的结论在小组内进行阐述,然后,小组内部要将所有的结论进行整合,从而总结探究出“圆内的点到圆心的距离小于半径,圆外的点到圆心的距离大于半径,圆上的点到圆心的距离等于半径”这个数学结论。每个区域的点到圆心的距离都可被认为是一个集合,这可以使学生初步掌握圆与一个集合之间的关系。然后,我让学生展开直线和圆的位置关系的自学活动,让学生如法炮制,学会学习,初步树立空间意识,掌握数形结合等相关数学思想方法。
三、加深学生的情感认知
初中生的思维活动以形象思维为主,数学学科强调的是抽象思维与逻辑思S,这就为初中生深入理解数学知识增加了难度。然而,数学知识来源于生活,是从生活中的具体事例中抽象出来的具有概括性的知识,因此,教师便可以利用生活中的数学元素,帮助他们顺利完成感性认识到理性认知的转变,加深他们对数学知识的认知程度。在学“圆”的相关知识的时候,我让学生指出圆在生活中应用的实际例子。学生指出车轮、自来水管、奥运五环等。在将这些实际例子的特点总结出来之后,展开探究,便可以帮助他们理解圆的概念、性质等抽象的数学知识。
总之,素质教育强调的是学生的主动探究、学习态度、学习品质等多方面的发展。因此,教师应该把教学重心放在培养初中生的数学学科素养方面。教师要注意培养初中生的探究意识,使其学会主动思考,提高他们质疑与解决问题的能力;教师要帮助初中生掌握科学的学习方式,使他们能够做到举一反三,减轻教师的教学负担;教师要利用生活中的数学元素,加深学生的情感认知,使其对数学在生活中的应用的感触更深,从而形成良好的数学品质。
参考文献:
关键词:基础数学;动态教学;教学效果
中图分类号:G642.0 文献标志码:A 文章编号:1674-9324(2014)39-0059-03
一、基础数学教学过程中的问题分析
数学不仅是各学科基础,更是人才素质的重要组成部分。数学类专业包括:数学与应用数学、信息与计算科学,统计学(现在是单独学科),其中基础数学课程主要包括:数学分析、高等代数、空间解析几何、常微分方程、复变函数、概率论、数理统计,近世代数等等;非数学类专业的基础数学课程主要包括:高等数学、线性代数、概率统计。数学在人才培养过程中的重要性是不言而喻的,作为基础数学课程的教学,如何适应高等教育大众化,不仅是基础数学课程教师要考虑的问题,更是各高校需要认真考虑并加以解决的问题。关于这方面的问题,各高校都有各自的矛盾和解决办法。总体来说各高校存在的普遍问题是:基础数学课程的教师比较紧缺,青年教师偏多,且以大班上课为主。另外,有的老师除了承担基础数学课程的教学任务外,还承担有专业课程的教学任务,使得部分教师课头多,教学任务重等各种因素,导致教学质量有所下降。由于基础数学课程是相关学科专业的重要基础课程,具有高度的基础性、抽象性、严密性、逻辑推理性等等,又有广泛的应用性,所以在基础数学课程的授课过程中主要以板书授课的形式为主,边讲边推理。基础数学课程的教学内容具有完整性,前后章节联系都比较密切,一环扣一环,所以每一次课讲得好坏都会影响到后面的教学效果,甚至打乱后面教学计划的执行。这也是我们在教学过程中经常遇到的问题。在基础数学课程的课堂教学过程中每一次的教学效果如何,部分教师很少考虑,有时根本不去考虑,等到布置作业后,通过学生做作业的情况,才会发现教学效果的情况。如果学生作业做得比较好,说明这次教学效果比较好;如果做得差,说明这次教学效果不理想,教学效果差,即使是这种情况,少数教师还认为是学生不好好学,很少反省自己的教学过程存在哪些问题。如果教师的作业比较多,不能及时地批改出来,通过作业暴露的问题往往就不能及时地纠正,导致问题的积累越来越多,必然会影响后面的教学。教学过程中暴露的问题还有很多,而暴露的这些问题通常都是在课后才发现的,有的甚至在课程结束后才发现教学有问题,由于受课时的限制很难进行补救。如果我们在讲课前对教学内容、方法和教学手段的效果进行预测,在教学效果预测的基础上,根据教学内容认真备课,安排好每一个教学环节;对教学效果在授课课前进行预测,把事后变为事前预测,这就是我们本文要探讨的基础数学课程的动态教学模式与课堂效果评价问题。
二、基础数学课程动态教学模式与教学效果预测
由于基础数学课程分前后内容联系都非常密切,甚至几次课的内容都是整体的一部分,所以,我们在授课的过程中不能孤立地去看待每一次的教学内容,而要考虑前后内容的衔接。以高等数学或数学分析为例,教材一般为上下两册,通常为两个学期或三个学期。高等数学或数学分析课程下册的无穷级数要用到上册数列极限的有关内容;下册的重积分、曲线与曲面积分、傅立叶级数等等要用到上册的定积分等等;导数的定义实际上就是极限问题;多元函数的许多性质是一元函数的推广,但又要注意其不同于区别。所以,我们在备课、讲课的过程中,不能只考虑这次课要讲的内容,还要考虑后面教学内容的连贯性。基础数学课程的教学过程可以分为两部分:教学计划,教学实施。根据基础数学课程教学内容,教学计划又分为:教学内容的总体计划,学期计划,月计划,周计划和每次课的计划。教学计划制订好以后,就要对基础数学课程的教学目的和要求进行预测。基础数学课程教学预测大致可以分为:教学内容的总体预测、学期预测、月预测、周预测。在预测的基础上,制订相应的教学目标,做到有的放矢。有了教学预测和教学目标,才能进行教学实施,教学实施主要包括备课、讲课、批改作业等等各环节。显然,对于基础数学课程的教学能否达到预期的教学目标,关键的是教学实施。根据基础数学课程的教学内容和教学特点,我们把教学实施分为以下几个阶段:教学效果预测(包括教学方法,教学手段,甚至例题的选择等等),备课(包括布置作业),授课,批改作业,课堂教学效果评价。教学效果预测是教学实施过程的前提,没有预测,教学过程就没有目标,也就谈不上教学质量;要达到一个什么样的教学目标、教学效果,必须要做到心中有数。有了教学效果预测,在备课时,就会考虑到各种教学方法和手段的可行性,避免失误。这样,一次课下来后,与预期的目标进行比较,如果达到或超过预期的目标,说明这次的教学是成功的,使用的教学方法、手段是可行的,否则,教学有问题,要及时反省,查找原因,下次课及时调整。教学效果评价不仅是自己教学水平的评价,也是提高教学水平的重要手段,更是对自己教学态度评价,同时它也是下次教学效果预测的依据。在教学效果评价的基础上,对下次的教学内容进行预测,并重复上述过程,这样我们就有下面教学实施的循环:
在备课之前,首先要对下次教学内容的教学效果进行预测。我们不仅要考虑下次课要讲哪些内容,还要考虑学生理解和掌握这些内容的情况进行分析、预测,以及教学过程中可能会出现的各种情况都要有充分的估计。对不同的教学内容或同一教学内容中的不同知识点,采用不同的教学方法其教学效果往往是不同的,哪一种教学效果比较好,都要进行分析和预测;如何讲好每一个知识点,如何讲解学生更容易理解、掌握等等,都是备课时需要认真考虑的,真正做到学生是授课过程的主体。教学效果预测要充分考虑学生对老师的愿望,因为老师授课的对象是学生,是教学过程的主导者。在讲课之前学生对老师也有一个期望,最低的要求就是希望老师所讲的内容清楚、能听懂,除此之外还有理解等等方面的要求。如果老师的授课能达到学生的要求,学生认为这位老师的授课水平高,否则就是这位老师授课水平低。但教师授课水平的高低目前没有一个明确的界限,以期末考试的试卷难易程度和学生考试的成绩来反映教师的教学水平也是不科学的,因为试卷的难易程度很难定论,是一个模糊的概念,凭感觉。如何鉴定教师授课水平,一直是困扰教学质量、教学效果评价的难题,为此,我们做了一些的探讨与实践,不一定科学。设x是任课教师对教学效果给出一个预测值,y是学生给任课教师期望值,如果x≥y,说明这位老师可以胜任这门课的教学。否则,这位教师不胜任这门课的教学任务,学生对该教师的评价不会太好的。这就是说老师对自己要高标准,在这种情况下才能发挥教学水平,提高教学效果。一般来说,在授课之前,学生不知道老师的教学效果预测值是多少,学生也不会给老师期望值。如果我们把教学效果的评价定量化,那么,教学效果的评价值可以看成x的函数f(x),当f(x)≥x时,说明这次的教学方法和教学手段应用得当,达到了预期的教学效果和目的;当f(x)
1.老师在上课前根据这次课的教学内容进行备课,并写出本次课的教案,下次上课前再根据要讲的教学内容进行备课,再写出该次课程的教案,也就是讲一次课备一次课的教学内容。这种备课省事,大部分老师都是采取这种方式,有利于上课时对本次课教学内容比较清楚。但不足的是:基础数学课程教学内容的部分完整性差;如果有次课上得不好,失误较大,或者讲得过快,或者讲得过慢,这样就不利于调整教学内容、教学方法、教学手段,灵活性差,会影响后面的教学内容、教学效果等等。
2.老师根据基础数学课程教学内容的部分完整性,备一次课,写几次课的教案,虽然这种备课方法对课堂教学内容的调整有一定的灵活性,一定程度上弥补了上一次课写一次教案的不足,但因时间较长,有时会对教学内容记得不太清楚、生疏,影响教学效果。
为了避免上述备课存在的问题,我们提出了动态的三次备课法:就是每次备课时,备三次课的教学内容,并写三次课的教案:第一次课的教案详写,第二次课的教案可以写得粗一些,第三次课的教案写得更粗一些。如果备课时,备两次课的教学内容,写两次课的教案,若第一次上课时有失误,就要修改第二次课的教学内容,第二次上课时就要弥补第一次造成的失误,这样第二次课的教学内容不一定能完成,也就会影响后面的教学进度,导致后面为了赶进度而影响教学效果。如果备课时,写四次以上课的教案,花在写教案的时间较多,也没有必要。教学实践证明,备课时写三次课的教案是科学的,因为第一次课有失误,在下面的两次课完全可以调整教学内容,不影响后面的教学进度。第一次课上完后,进行教学效果评价,在评价的基础上,调整第二次教案的教学内容,并写出详细的教案,同时修改下次教案,增加一次较粗的教案。如此滚动下去,每次备课都保证有三次详、粗适当的教案。
动态备课法模式:
第一次备课
3.基础数学课程课堂教学效果评价。在前面,我们提到了课堂教学效果评价,它是下一次课堂教学效果预测的前提和基础,是评价课堂教学好坏的主要论据,也是备课时必须考虑的重要因素。虽然影响课堂教学效果的因素很多,有些是不可预测的,但最重要的因素应该是教师。我们知道,基础数学课程的课堂教学以讲课为主,概念、推理、举例等等都是边写边讲,在讲解的过程中速度不能过快,也不能太慢,如果老师讲得好,那么学生喜欢听,注意力集中,效果肯定好;如果老师讲得不好,那么,有的学生会产生厌学等情绪,思想不集中,学生出于课堂纪律的约束,会表现出心不在焉的听课样子。从学生的课堂表现,可以感觉不出来自己讲得是好还是不好,是判断课堂教学效果的依据,但不能就此给自己的教学效果做出正确的评价。如何对自己的教学效果做出正确的评价,评价的依据是什么,目前还没有合理的说法和理论依据。目前大多数的做法是通过学生的考试成绩,学生对老师的打分,以及督导组的老师听课等等来说明老师的教学水平。这种评价看似有道理,但是不全面的。基础数学课程是大面积公共基础课,考试时统一试卷;影响学生考试成绩的因素很多,考题的题量、难易度,生源,专业的要求和培养目标,学风等等,都是影响考试成绩的因素。学生给老师打分也存在许多缺陷和不公正,课堂教学管理严的老师得分不一定高,要求不严的老师可能得分较高;有的学生对老师的评价无所谓,尽量打高一点。督导老师打分往往是表面印象,如果不是同行专家更是如此。所以,最具有说服力的评价是自己给自己评价。如何给出一个合理的自我评价,一直是教师都想搞明白的事,特别是一次课下来后,这次课上得如何等等,都是值得研究的问题。经过多年的教学研究和教学实践说明,学生上课时的情绪、提问以及学生的作业,是反映教师课堂教学效果的主要依据。学生上课时的情绪可以反映教师讲课的激情、语言的表达、内容的安排、概念的讲解、教学手段的使用、教学方法是否恰当等等,所以在上课时一定要注意学生的情绪。课堂提问可以及时了解学生对知识掌握的情况,更能反映老师的教学水平。课堂提问一般分为直接提问和间接提问,直接提问就是请同学站起来回答问题,适应于小班上课;间接提问就是老师在上课过程中提出问题,然后看学生对老师提的问题反映表情来判断学生掌握的情况,这种提问适应于大班上课,最好是直接提问与间接提问并用。作业不仅可以反映学生平时成绩,更能反映教师课堂教学效果的好坏,它是定量反映老师这次课教学效果情况的具体表现。所以布置作业一定要认真,要求学生都是独立完成作业,不要给出参考答案,且作业布置要注意难易程度、题量适度,一个教师教学水平如何从作业上基本上可以反映出来。为了更好地分析课堂教学效果,根据上面的分析可以定量地进行评价自己这次教学效果,即教学效果评价成绩=上课时学生的课堂情绪20%+课堂提问10%+作业70%。上课时学生的课堂情绪成绩和提问成绩根据上课时的表现来给出,作业成绩为批改作业的平均成绩,也可以随机地抽取一定比例的作业平均成绩作为作业成绩。由于我们在上课前对教学效果进行了预测,并给出一个预测值。当预测值≤教学效果评价成绩,说明这次教学是成功的,达到了预期效果;当预测值>教学效果评价成绩,说明这次教学有问题,必须认真查找原因,在下面的教学过程中纠正。这样我们就给出了课堂教学效果的计算公式:课堂教学效果值=课堂教学效果评价―课堂教学效果预测。当课堂教学效果值≥0,说明这次教学是成功的,达到了预期效果;当课堂教学效果值
总之,要保证教学质量,提高教学水平,关键是提高课堂教学效果。作为一名教师首先要加强课堂教学管理,对自己的教学情况要有一个合理的评价,才能不断提高教学水平和能力。如何加强课堂教学管理,并对教学效果进行预测和评价,我们进行了研究并在教学过程中进行探讨,得到了上述的成果,特别是对数学课程的教学有一定的推广价值。
参考文献:
[1]严振祥.高等数学大班课教学的对策[J].大学数学,2007,23(2):25-26.
[2]王庆.对高等数学分层教学的探讨[J].科技创新导报,2008(9):240.
[3]董勇,.高等数学课程特点与教学改革初探[J].长江大学学报:社会科学版,2009,32(2):242-243.
关键词:创新意识 创新能力 趣味数学 开发思维
一、创设生活情境小学生的思维以形象为主
数学教育是要学生获得作为一个公民所必须的基本数学知识和技能,为学生终身可持续发展打好基础,必须开放小教室,把生活中的鲜活题材引入学习数学的大课堂。例如在教学了圆柱体和圆锥体的体积后,我出示了一个不规则的物体,要求学生想办法求出它的体积。学生通过认真的讨论交流,设计出了一个计算这不规则物体体积的方案:先将一个容器里放一些水,然后测量并计算出现在容器中水的体积,再将不规则的物体放入容器中,再测量并计算出放入不规则物体后现在容器中水的体积,容器内水的前后体积的差即为这不规则物体的体积。这样通过交流、讨论、合作等学习方式,既可培养了学生良好的与别人沟通的能力,也可培养学生的探索思维能力。这样既提高了学生学数学的兴趣,也培养了学生的创新能力和创新意识。
二、创设联系生活实际的作业
学生经过教学和课堂练习掌握了一些知识,虽然也能解决一些简单的实际问题,但因为这些实际问题都经过加工处理过,学生往往很快会忘记,如果能联系生活实际设计一些作业,学生形象深刻,会容易记住。如在教学了长方体和正方体的体积后,因为学生对于占地面积和表面积极容易混淆,我拿出六块同样大小的木板,并请学生量出三块木板的长、宽和高,做两次安放:第一次将三块木板并列平放在地上,我请学生计算出这时三块木板的总占地面积是多少平方厘米?然后我再将另外三块木板重叠平放在一起,放在地上,再请学生计算出这时三块木板的占地面积是多少平方厘米,通过计算,学生很快知道,三块木板重叠平放在一起放时的占地面积小,占地面积的大小同木板的表面积并无关系。这样使学生对占地面积和表面积这两个概念加深了理解。
我再请学生思考将三块木板并列放在地上,这时三块木板的表面积和是多少平方厘米?将三块木板重叠平放在一起时,三块木板的表面积和又是多少平方厘米?我再将三块木板竖着重叠放和横着重叠放,并请学生根据已知的数据分别求出三块木板平着重叠放、竖着重叠放和横着重叠放时三块木板的表面积和各是多少平方厘米?这样使得学生既较好地掌握了表面积的概念,并使学生懂得了不同的放法表面积是不同的。为了加深学生对表面积和体积概念的掌握,我还要求每个学生从家中拿来一只火柴盒,让学生量出它的长、宽和高,并提问学生,火柴盒的内盒如果不拿出来,这时求它的表面积要求几个面?如果将内盒拿出来,不计火柴盒的厚度,求做一只内盒要多少材料?要求几个面?这时相当于求什么?如果求火柴盒的外壳要用多少材料,又要求几个面?这时又相当于求什么?在火柴盒上做商标,只要求出什么?这只火柴盒占空间的大小是多少?如果火柴盒的厚度忽略不计,这只火柴盒的容积又是多少?火柴盒的体积和它的容积相等吗?火柴盒的容积和体积在什么时候相等?什么情况之下不相等?学生联系实际并经过讨论、交流和合作,很快能将这些问题一一解决,并会认识到,火柴盒里面有很多的学问。这样使得学生不仅再次加深了对侧面积、表面积、体积和容积的理解,并联系火柴盒还知道了在实际生活中运用数学要考虑很多因素。同时,也使学生的创新能力和创新意识有了提高。
三、联系实际、创设生活化的数学情境在数学教学中
如何让学生置身于逼真的问题情境中,体验数学学习与实际生活的联系,品尝到用所学知识解释生活现象以及解决实际问题的乐趣,感受到借助数学的思想方法,学生会对生活中常见的各种优惠措施理解得更深刻,真正体会到学习数学的乐趣。因此在数学教学中,我努力尝试在数学教学过程中加强实践活动,使学生有更多的机会接触生活和生产实践中的数学问题,认识现实中的问题和数学问题之间的联系与区别。例如,在教学了“用字母表示数”后,我设计了这样一题“开放性”的实践题:“学校在暑期组织教师前往北京进行七日游活动,无锡到北京的火车票为X元,教师在火车上和在北京每天的伙食费为B元,要在北京住宿5夜,每夜的住宿费为A元,在北京的旅游点的门票价和交通费共计为Y元,问每个教师去北京旅游共需要多少元钱?”我先请学生用字母表示数,写出每个教师去北京旅游共需要多少元钱。学生很快能写出每个教师去北京旅游需要钱的算式:2X+7B+5A+Y.在学生写出了算式后,我还要求学生能联系实际查找资料,估算一下每个教师前去北京共要用多少元钱?这样学生就会前去查找无锡到北京的火车票价,去了解每天的伙食费和住宿费是多少元。
通过这样的教学,不仅调动了学生学习数学的积极性,而且使学生体会到了创新来自实践的道理,同时也培养了学生的创新能力。
目前高职数学教学在教学模式、课程设置、教学内容、教学方式等方面都存在很多问题,已不适应当前职业教育的培养目标,主要表现在以下几方面:
一、高职数学基础教学的现状
目前高职数学教学在教学模式、课程设置、教学内容、教学方式等方面都存在很多问题,已不适应当前职业教育的培养目标,主要表现在以下几方面:
1、传统的教育观念难以满足高职教育人才培养目标的要求
传统的数学教育观念以“知识本位”为中心,偏重理论知识的完整性、系统性和严密性,注重使学生获得比较系统的知识,但是轻视理论知识的应用性和实践性。这种传统的“知识本位”的教育理念,难以满足高职教育人才培养目标的要求。
2、教学内容陈旧,难以满足专业需要
传统的高职数学教学内容体系一成不变,所有专业都使用一本教材,数学课与专业课脱节,容易使学生产生“学而无用”的厌学心理。教学内容体系强调知识的系统性,理论上追求严谨,内容上要求面面俱到,造成内容多、课时少的矛盾,致使数学教学内容难以满足各专业的要求,不能为后继专业课的学习打好基础。
3、教学方式单一,不能满足现代化社会的需要
“一本教材,一个教案,一支粉笔教一辈子”的教学方式已不能满足现代化社会的需要。高职数学教学如果不采用多媒体教学,增设数学实验课,培养学生的数学建模能力,那么他们所学的数学技能将难以满足未来职业的需要。
二、数学教学实践中的创新分析
“以服务为宗旨,以就业为导向”,紧紧围绕专业课程设置数学教学内容,充分体现了高职教育的特色。我们通过问卷调查分析学生的入学水平、对数学的学习兴趣,摸清学生的基本情况,有针对性地进行教育改革。在今后的实践中我们将改革数学教学内容体系,精选符合各专业要求的教学内容,建立起一套满足专业需求,促进学生职业发展的教学内容体系。
1、转变观念,树立高职数学为专业服务,以专业为本的思想
教师作为教育改革的实施者,应转变传统的“纯数学理论”教学观,树立为专业服务的意识。不断了解最新的数学发展动向及专业中的新成就,及时地将现代数学知识纳入数学教学体系中,为学生构建适应现代社会的知识体系。同时还应教会学生应用先进的数学计算软件,使学生学会利用先进的数学计算工具学习数学,用数学解决专业中的计算问题,使数学教育真正体现“以应用为目的”的教学原则。
2、构建符合专业要求的数学教学内容体系,以实践教学引导学生主动学习运用多媒体技术和网络技术体现全方位教学
引进现代教育技术是提高教学质量的重要手段,采用多媒体教学,优化课堂教学,提高教学效率和教学效果。改变单一的课堂教学模式,打破数学课只有习题课,培养学生利用科学计算方法与手段处理数据的能力。调查不同专业对高等数学课程的要求,确定教学内容体系和教材。根据专业需要精选高等数学经典教学内容,引进与专业相关的现代数学知识,使教学内容富有时代气息,构建富有时代特色的满足人才培养目标的教学内容体系。
3、更新教学组织形式,渗透数学的思想方法
教学中应改变传统的以公式、定理、性质为主的教学方法,以案例讲解为主,结合实际问题的处理介绍数学的基本概念。淡化数学体系的系统性、逻辑性和完整性,强调一个“用”字。应从素质教育和高职人才培养目标出发,根据不同专业,削减与专业关系不大的内容,增添必要的新内容,体现以必须够用为度的一个“度”字。这样一方面提高了学生的学习兴趣,另一方面也使学生学到了更多的数学的“精髓”。
4、数学的学习不应只是局限于课堂
随着网络的发展,网上学习与答疑也是获得知识的重要途径,组建数学建模小组,建立网上课堂,充分利用和发挥计算机多媒体辅助教学(CAI)的作用,这些都可以激发学生的学习积极性,提高学生的数学学习水平。
三、通过一年多高职数学教学内容体系的实验研究,我们有一些体会
1、打破课程体系优化教学内容,有利于实现培养目标
教学内容的改革体现了数学为专业服务的思想,强调了数学的基本概念和基本理论在各自专业中的实际应用,更有利于培养具有较强实践能力的技术应用型人才。教师要做到体现“教师是主导,学生是主体”的原则,不但能够传授知识,而且更重要的是引导学生自学与交流、提高学生的创造性思维能力和指导学生的实践科学研究。
2、教学内容的更新,有利于培养学生的现代数学应用能力
数学与计算机有机结合,将数学实验与数学建模思想融入到经济数学教学内容中,可以使学生切实感觉到数学在处理经济问题中的巨大作用,从而使学生逐步具备现代数学应用能力。
3、教学方法组织形式的改革,有利于调动学生的学习积极性
努力建设“和谐课堂”,提倡“以人为本”的教学理念,改变传统的教学方法,调动学生的参与性,对激发学生学习兴趣调动学生学习积极性具有重要作用。强调学生在教学过程中的主体地位。立足于数学课程的实用性和专业融合性,在课程设置、教学模式、教学方法、评价制度等方面做出积极的探索。
高职数学教学内容体系的改革必须准确把握高职教育的培养目标,以教育思想观念改革为基础,以专业知识为导向,探讨具有高职专业色的教学内容体系。这是一项长期的艰巨的系统工作,只有反复探索,认真实践,才能建立适应现代高职教育的数学教学体系。
参考文献:
关键词:微积分;背景;作用;函数
一、微积分进入高中课本的背景及必要性
在数学发展史上,自从牛顿和莱布尼茨创建微积分以来,数学中的很多问题都得以解决。微积分已成为我们学习数学不可或缺的知识。其在经济、物理等领域的大量运用也使之成为解决生活实际问题的重要工具。但牛顿和莱布尼茨创建的微积分为“说不清”的微积分,也就是连他们自己也说不清微积分的理论依据,只是会应用。这使得很多人学不懂微积分,更不用说让中学生来学习微积分。
柯西和维尔斯特拉斯等建立了严谨的极限理论,巩固了微积分基础,这是第二代微积分,但概念和推理繁琐迂回,对高中生更是听不明白。近十年来,在大量的数学家如:张景中,陈文立,林群等的不懈努力下,第三代微积分出现了相比前两代说得清楚,对高中生而言,也更容易理解。这为其完全进入高中课本奠定了基础。从内容来看,新一轮的课改数学教材在微积分部分增加了定积分的 概念及应用(求曲边梯形面积,旋转体体积,以及在物理中的应用),可能考虑到中学生的认知能力,人教版新教材与北师大版在这方面有所不同。即利用定积分求简单旋转体体积在北师大版教材中出现了,但人教版没有。
从课标和考试大纲(参考2011年高考考试大纲)上看,初等微积分所占比重也是越来越重。回顾历届高考,微积分相关题型分值越来越高。但就我个人观点,初等微积分在中学数学中的作用还没有真正全面发挥。我认为,它是学生中学数学和教师教学的一条线索,它是我们研究中学函数问题的统一方法,也是联系中学与大学数学知识的纽带!
二、微积分在中学数学中的作用
1.衔接性与后继作用。微积分本是大学高等数学范畴,是大学开设的课程。让现在中学生提前学习部分微积分知识,这便为其以后升入大学学习微积分打下良好的基础,这也使数学知识从小学到大学从内容上衔接得更加紧密。也不会再出现很多大学生认为的大学数学知识在高中数学教学中没有任何作用的观点.
2.解决数学相关知识的作用。高中数学函数在整个中学数学内容中,不论从高考所占比重还是自身难度来说都应该排在首位。对学生来说永远是最难学的,得分率也相对比较低。很多学生讨厌数学就是讨厌函数,提到数学中的函数就头晕。由于应试教育的关系,学生又不得不学习函数,而函数思想本身也是高中数学学习的一条线索。微积分的进入对学生学习函数问题找到了统一的方法。高中阶段我们所研究的函数问题一般是以一些基本初等函数为媒介研究函数的定义,图像和性质,当然也有应用。但随着课改的深入,函数应用问题逐渐在淡化。而初等微积分知识即研究函数的重要工具,如:微积分可以求函数的单调性,最值。最重要的是它可以画出函数的图像,其实,当函数图像画好后,几乎函数所有性质都可以解决。学生只要学好微积分便掌握了研究函数的统一方法,那么高中阶段的二次函数,指数函数,对数函数,三角函数等所有初等函数的学习就可以统一,既节约了教学时间又学习了先进的数学思想。对提高学生的数学修养打下坚实的基础。我相信还可以激发其学习数学的兴趣。另外,在高中阶段,初等微积分还可以解决不等式问题,求二次曲线的切线问题,求曲边梯形的面积等很多数学问题。利用微积分不仅可以使问题简化,并能使问题的研究更为深入、全面。
3.提高数学在其他学科的应用能力。作为自然学科的数学本身已应用于社会经济、技术等各个领域。而作为中学数学,它对中学其它学科的推动作用也是毋庸置疑的。如物理,化学,地理等学科也离不开数学。在高中阶段往往会因为数学的教学进度而影响其它学科的进度。如地理中要学习地球的经度,纬度等知识就需要先学习数学中球体相关知识和解三角形相关知识。当微积分进入中学数学后,数学这个学科的作用就更加重要了。特别像物理中匀加速直线运动位移,瞬时速度,加速度等问题利用微积分的导数求解起来更加简单,容易理解。新课程人教版数学教材选修2-2中专门加入了利用定积分求变速直线运动的路程一节。另外,微积分解决生活中的优化问题也进入中学课本。可见,微积分进入中学教材,对促进学科间知识的整合起到了至关重要的作用。
三、国际上一些教材对微积分知识的处理
关键词 整合 整合的定位 新型教学方法
中图分类号:G633.67 文献标识码:A 文章编号:1002-7661(2017)08-0053-02
教学改革的全面展开和信息技术的深人应用,催化了课堂教学模式的变革。如何实现信息技术教育与数学学科的整合,是每一个数学教师要面对的重要的和长期的课题之一。
一、对信息技术教育与学科整合的理解
信息技术教育和课程的整合从宏观的角度,就是要把学生要掌握的学科教学目标和信息技术素养目标结合起来,在实现学科教学目标的过程中同时实现信息技术素养目标。从微观的角度,就是信息技术与具体教学过程的整合。即在课程教学中把信息技术、信息资源、信息方法和课程内容有机结合,共同完成课程教学任务的一种新型教学方法。
二、整合的必要性
“信息技术与课程的整合”是我国面向21世纪基础教育教学改革的新视点。《数学课程标准》指出:“数学课程的设计与实施应重视运用现代信息技术,改变学生的学习方式,使学生乐意并有更多的精力投入到现实的、探索性的数学活动中去。”由于传统教学的局限性,制约着教学质量的提高,即整合是提高教学质量和素质教育所要采取的必要手段。因此,信息技术与数学学科的整合是教学改革的要求,也是时展的要求。
三、信息技术在数学课堂教学的优势
1.信息技术变“学数学”为“做数学”
传统教育片面强调逻辑思维训练,忽视对观察、实验、想象、猜测等能力的培养;忽视学生的内心活动、情感体验和合作交流;重视对结果的应用而忽视对过程的探究。教师经常代替学生思维,结果本来生动、机智、充满创造力的整个数学思维过程不见了,导致学生认为数学不过是一些纯粹的理论和枯燥的运算和证明,没有多少实际用处。现在,信息技术为数学教学开创了一个“数学实验室”,利用“几何画板”教育平台和其他工具软件,为学生“做”数学提供必要的工具与手段,让学生可以自主地在“问题空间”里进行探索,来做“数学实验”。这样我们也向:“一个差的老师给人奉送真理,而一个好的老师教人发现真理。”的发展更进了一步。
2.动态图象有利于突破教学重点和难点
信息技g与数学课程的整合可使抽象的概念具体化、形象化,尤其是计算机能进行动态的演示,弥补了传统教学方式在直观感、立体感和动态感等方面的不足,利用这个特点可处理其他教学手段难以处理的问题,并能引起学生的兴趣,增强他们的直观印象,为教师化解教学难点、突破教学重点、提高课堂效率和教学效果提供了一种现代化的教学手段。
3.课堂教学效率显著提高
上数学课总是免不了要画图,这些作图中有部分是机械的、重复的,有些还相当繁复,并且有时作图本身对达到该节课的教学目标的意义并不大。如:“图形的平移”,先告诉计算机平移方向及平移距离(一个向量即可),再选中平移对象即可完成平移,既简单、明了,又直观、形象。用计算机代替老师、学生做这些工作,既彻底减轻了负担,让教师、学生把精力和注意力用到更高层次的教学和学习环节中去,同时也有助于师生更了解和熟悉信息技术,使教学效果显著提高。
四、整合的定位
1.要与数学的学科特点相结合,突出数学的思维特点
数学具有逻辑的严密性、高度抽象概括的理论,并大量使用形式化、符号化的语言。学习数学、解决问题的过程是一个思维活动的过程。揭示思维过程、促进学生思考领悟成为数学教学的特殊要求。因此,整合必须与数学的学科特点相结合。信息技术在数学课堂教学的运用一定要紧扣教学目标和教学内容,要根据不同的教学目标和教学内容的特点去选择、运用不同的信息技术,充分发挥其在教学上的优势,不能把数学搞成电脑多媒体功能的成果展览。总之整合中,我们关心的不是信息技术,而是课程本身。
2.应以服务学生的学习为中心,变辅教为辅学
整合应清晰地认识到,信息技术是学生更有效地获取知识、发展智能的一种工具。强调信息技术要服务于数学学习,要成为学生学习的工具。使用信息技术的出发点是利用好信息技术的优势,促进学生思维,利于学生学习数学知识。
一、信息技术与初中数学教学的整合是时代的要求
初中数学教育信息化建设对于转变初中数学教育思想和观念,促进初中数学教学改革,加快初中数学教育发展和管理手段的现代化都有积极作用,尤其是对于深化基础教育改革,提高九年义务教育质量和效益,培养“面向现代化,面向世界,面向未来”的创新人才更具深远的意义。初中数学教育信息化建设过程及其全方位应用,不仅是改革传统教育模式的有效途径,更是提高国民素质的重要措施,是中华民族真正融入国际社会的必由之路。
二、充分认识信息技术在数学课堂教学中的优势
1.信息技术变“学数学”为“做数学”。现代数学教育强调要进行“问题解决”,在解决问题过程中锻炼思维、提高应用能力。现在,信息、技术为数学教学开办了一个“数学实验室”,为学生“做”数学提供必要的工具与手段,让学生可以自主地在“问题空间”里进行探索,来做“数学实验”。教师可以将更多的探索、分析、思考任务交给学生去完成;学生从“听”数学的学习方式改变成在教师的指导下“做”数学;过去被动接收“现成”的数学知识,而现在可以像“研究者”一样去发现探索知识。
2.动态图像有利于突破教学重点和难点。计算机辅助教学进入课堂,可是抽象的概念具体化、形象化,尤其是计算机能进行动态的演示,弥补了传统教学方式在直观感、立体感和动态感等方面的不足,利用这个特点可处理其他教学手段难以处理的问题,并能引起学生的兴趣,增强他们的直观印象,为教师化解教学难点、突破教学重点、提高课堂效率和教学效果提供了一种现代化的教学手段。
3.课堂教学效率显著提高。数学总是离不了画图,这些作图中有部分是机械、重复的,有些还相当繁复,并且有时作图本身对达到该节课的教学目标的意义并不大。用计算机代替老师、学生作图,既彻底减轻了负担,让教学、学生把精力和注意力用到更高层次的教学和学习环节中去,同时也有助于师生更了解和熟悉信息技术,使教学效果显著提高。
三、运用信息技术激发学生的学习兴趣
“兴趣是最好的老师”,以前的课堂教学,我都是通过口头表述来组织教学,难以展现真实的生活情境,更别说激起学生的兴趣。而通过信息技术就能创设激发学生学习的情境。有了兴趣,学生才能在教师的引导下去观察、探究,从而有所发现,教学效果也随之提高。例如:在教学《数据的收集和整理》时,教材要求统计某路口在10分钟内各种机动车辆通过的数量,并制成统计表和条形统计图。如果只通过我的表述是难以描绘这一场景、营造学习氛围的,于是,我通过多媒体课件,向学生演示了一幅情景交融的画面,让学生非常直观地看见一辆辆摩托车、小汽车、大客车、载重车通过路口,学生的学习兴趣顿时高涨,充分体现了实践收集数据的真实感,从而轻松地投入到了学习中。看到学生兴奋的样子,我也为信息技术优化了我的课堂教学而深深感动着。
四、运用信息技术发挥学生的主体作用
讲授法是教育历史上最悠久,应用最普遍的方法。在我们以前的授课时,运用最多的就是讲授法。讲授法能在较短的时间内让学生获得大量系统的科学知识。但这种方式在大部分情况下都变成了注入式或填鸭式。从认知心理学看,数学学习是每个学生在各自不同的数学世界里,主动进行分析、吸收的过程。这表明了学生在数学学习活动中的主体地位。“双主教学模式”是目前一种较为科学的教学方式。这种模式因为有了信息技术的加入使学生的主体地位得到更好地体现。例如,在九年级《相似形》中,要求学生判断哪些图形形状相同大小不同,从而引出相似图形的概念。我先利用Powerpoint软件展示出大小不同形状相同的五角星等图案由学生辨认进而得出定义。在课堂教学中,这些鲜艳、明亮的图片对学生的视觉冲击力很大,他们的积极性都很高。相似形的定义给出后,学生自己利用几何画板或者word软件画出不同的图形。同学之间相互提问,进一步巩固所学的知识。又如讲到统计图的知识时,我让学生利用Excel软件对图表以及不同的图如柱形图,折线图之间进行转化。在教学中,我尊重学生的想法,创新的观点,给学生创造表现自我,展现自我的机会。在这样的学习过程中,体现了教师的主导作用,更重要的是学生的主体作用得到了充分的发挥。
五、运用信息技术营造热烈的探究氛围