发布时间：2022-02-26 13:22:17
序言：写作是分享个人见解和探索未知领域的桥梁，我们为您精选了8篇的数学知识点总结样本，期待这些样本能够为您提供丰富的参考和启发，请尽情阅读。
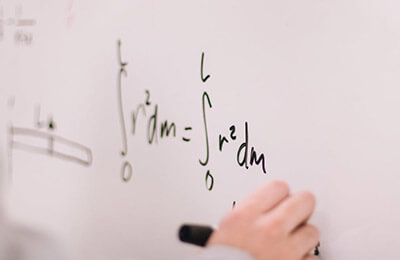
体积和表面积
三角形的面积=底高2。 公式 S= ah2
正方形的面积=边长边长 公式 S= a2
长方形的面积=长宽 公式 S= ab
平行四边形的面积=底高 公式 S= ah
梯形的面积=(上底+下底)高2 公式 S=(a+b)h2
内角和：三角形的内角和=180度。
长方体的表面积=(长宽+长高+宽高 ) 2 公式：S=(ab+ac+bc)2
正方体的表面积=棱长棱长6 公式： S=6a2
长方体的体积=长宽高 公式：V = abh
长方体(或正方体)的体积=底面积高 公式：V = abh
正方体的体积=棱长棱长棱长 公式：V = a3
圆的周长=直径 公式：L=r
圆的面积=半径半径 公式：S=r2
圆柱的表(侧)面积：圆柱的表(侧)面积等于底面的周长乘高。公式：S=ch=rh
圆柱的表面积：圆柱的表面积等于底面的周长乘高再加上两头的圆的面积。 公式：S=ch+2s=ch+2r2
圆柱的体积：圆柱的体积等于底面积乘高。公式：V=Sh
圆锥的体积=1/3底面积高。公式：V=1/3Sh
算术
1、加法交换律：两数相加交换加数的位置，和不变。
2、加法结合律：a + b = b + a
3、乘法交换律：a b = b a
4、乘法结合律：a b c = a (b c)
5、乘法分配律：a b + a c = a b + c
6、除法的性质：a b c = a (b c)
7、除法的性质：在除法里，被除数和除数同时扩大(或缩小)相同的倍数，商不变。 O除以任何不是O的数都得O。 简便乘法：被乘数、乘数末尾有O的乘法，可以先把O前面的相乘，零不参加运算，有几个零都落下，添在积的末尾。
8、有余数的除法： 被除数=商除数+余数
方程、代数与等式
等式：等号左边的数值与等号右边的数值相等的式子叫做等式。 等式的基本性质：等式两边同时乘以(或除以)一个相同的数，等式仍然成立。
方程式：含有未知数的等式叫方程式。
一元一次方程式：含有一个未知数，并且未知数的次 数是一次的等式叫做一元一次方程式。学会一元一次方程式的例法及计算。即例出代有的算式并计算。
代数： 代数就是用字母代替数。
代数式：用字母表示的式子叫做代数式。如：3x =ab+c
分数
分数：把单位1平均分成若干份，表示这样的一份或几分的数,叫做分数。
分数大小的比较：同分母的分数相比较，分子大的大，分子小的小。异分母的分数相比较，先通分然后再比较;若分子相同，分母大的反而小。
分数的加减法则：同分母的分数相加减，只把分子相加减，分母不变。异分母的分数相加减，先通分，然后再加减。
分数乘整数，用分数的分子和整数相乘的积作分子，分母不变。
分数乘分数，用分子相乘的积作分子，分母相乘的积作为分母。
分数的加、减法则：同分母的分数相加减，只把分子相加减，分母不变。异分母的分数相加减，先通分，然后再加减。
倒数的概念：1.如果两个数乘积是1，我们称一个是另一个的倒数。这两个数互为倒数。1的倒数是1，0没有倒数。
分数除以整数(0除外)，等于分数乘以这个整数的倒数。
分数的基本性质：分数的分子和分母同时乘以或除以同一个数(0除外)，分数的大小
分数的除法则：除以一个数(0除外)，等于乘这个数的倒数。
真分数：分子比分母小的分数叫做真分数。
假分数：分子比分母大或者分子和分母相等的分数叫做假分数。假分数大于或等于1。
一.知识归纳：
1.集合的有关概念。
1)集合(集)：某些指定的对象集在一起就成为一个集合(集).其中每一个对象叫元素
注意：①集合与集合的元素是两个不同的概念，教科书中是通过描述给出的，这与平面几何中的点与直线的概念类似。
②集合中的元素具有确定性(a?a和a?a，二者必居其一)、互异性(若a?a，b?a，则a≠b)和无序性({a,b}与{b,a}表示同一个集合)。
③集合具有两方面的意义，即：凡是符合条件的对象都是它的元素;只要是它的元素就必须符号条件
2)集合的表示方法：常用的有列举法、描述法和图文法
3)集合的分类：有限集，无限集，空集。
4)常用数集：n，z，q，r，n*
2.子集、交集、并集、补集、空集、全集等概念。
1)子集：若对x∈a都有x∈b，则a b(或a b);
2)真子集：a b且存在x0∈b但x0 a;记为a b(或 ，且 )
3)交集：a∩b={x| x∈a且x∈b}
4)并集：a∪b={x| x∈a或x∈b}
5)补集：cua={x| x a但x∈u}
注意：①? a，若a≠?，则? a ;
②若 ， ，则 ;
③若 且 ，则a=b(等集)
3.弄清集合与元素、集合与集合的关系，掌握有关的术语和符号，特别要注意以下的符号：(1) 与 、?的区别;(2) 与 的区别;(3) 与 的区别。
4.有关子集的几个等价关系
①a∩b=a a b;②a∪b=b a b;③a b c ua c ub;
④a∩cub = 空集 cua b;⑤cua∪b=i a b。
5.交、并集运算的性质
①a∩a=a，a∩? = ?，a∩b=b∩a;②a∪a=a，a∪? =a，a∪b=b∪a;
③cu (a∪b)= cua∩cub，cu (a∩b)= cua∪cub;
6.有限子集的个数：设集合a的元素个数是n，则a有2n个子集，2n-1个非空子集，2n-2个非空真子集。
二.例题讲解：
【例1】已知集合m={x|x=m+ ,m∈z},n={x|x= ,n∈z},p={x|x= ,p∈z}，则m,n,p满足关系
a) m=n p b) m n=p c) m n p d) n p m
分析一：从判断元素的共性与区别入手。
解答一：对于集合m：{x|x= ,m∈z};对于集合n：{x|x= ,n∈z}
对于集合p：{x|x= ,p∈z}，由于3(n-1)+1和3p+1都表示被3除余1的数，而6m+1表示被6除余1的数，所以m n=p，故选b。
分析二：简单列举集合中的元素。
解答二：m={…， ，…}，n={…， , , ，…}，p={…， , ，…}，这时不要急于判断三个集合间的关系，应分析各集合中不同的元素。
= ∈n， ∈n，∴m n，又 = m，∴m n，
= p，∴n p 又 ∈n，∴p n，故p=n，所以选b。
点评：由于思路二只是停留在最初的归纳假设，没有从理论上解决问题，因此提倡思路一，但思路二易人手。
变式：设集合 ， ，则( b )
a.m=n b.m n c.n m d.
解：
当 时，2k+1是奇数，k+2是整数，选b
【例2】定义集合a*b={x|x∈a且x b}，若a={1,3,5,7},b={2,3,5}，则a*b的子集个数为
a)1 b)2 c)3 d)4
分析：确定集合a*b子集的个数，首先要确定元素的个数，然后再利用公式：集合a={a1，a2，…，an}有子集2n个来求解。
解答：a*b={x|x∈a且x b}， ∴a*b={1,7}，有两个元素，故a*b的子集共有22个。选d。
变式1：已知非空集合m {1,2,3,4,5}，且若a∈m，则6?a∈m，那么集合m的个数为
a)5个 b)6个 c)7个 d)8个
变式2：已知{a,b} a {a,b,c,d,e},求集合a.
解：由已知，集合中必须含有元素a,b.
集合a可能是{a,b},{a,b,c},{a,b,d},{a,b,e},{a,b,c,d},{a,b,c,e},{a,b,d,e}.
评析 本题集合a的个数实为集合{c,d,e}的真子集的个数，所以共有 个 .
【例3】已知集合a={x|x2+px+q=0},b={x|x2?4x+r=0},且a∩b={1},a∪b={?2,1,3},求实数p,q,r的值。
解答：a∩b={1} ∴1∈b ∴12?4×1+r=0,r=3.
∴b={x|x2?4x+r=0}={1,3}, a∪b={?2,1,3},?2 b, ∴?2∈a
a∩b={1} ∴1∈a ∴方程x2+px+q=0的两根为-2和1，
∴ ∴
变式：已知集合a={x|x2+bx+c=0},b={x|x2+mx+6=0},且a∩b={2},a∪b=b，求实数b,c,m的值.
解：a∩b={2} ∴1∈b ∴22+m?2+6=0,m=-5
∴b={x|x2-5x+6=0}={2,3} a∪b=b ∴
又 a∩b={2} ∴a={2} ∴b=-(2+2)=4,c=2×2=4
∴b=-4,c=4,m=-5
【例4】已知集合a={x|(x-1)(x+1)(x+2)>0},集合b满足：a∪b={x|x>-2}，且a∩b={x|1
分析：先化简集合a，然后由a∪b和a∩b分别确定数轴上哪些元素属于b，哪些元素不属于b。
解答：a={x|-21}。由a∩b={x|1-2}可知[-1,1] b，而(-∞,-2)∩b=ф。
综合以上各式有b={x|-1≤x≤5}
变式1：若a={x|x3+2x2-8x>0}，b={x|x2+ax+b≤0},已知a∪b={x|x>-4}，a∩b=φ,求a,b。(答案：a=-2，b=0)
点评：在解有关不等式解集一类集合问题，应注意用数形结合的方法，作出数轴来解之。
变式2：设m={x|x2-2x-3=0},n={x|ax-1=0}，若m∩n=n，求所有满足条件的a的集合。
解答：m={-1,3} , m∩n=n, ∴n m
①当 时，ax-1=0无解，∴a=0 ②
综①②得：所求集合为{-1，0， }
【例5】已知集合 ，函数y=log2(ax2-2x+2)的定义域为q，若p∩q≠φ，求实数a的取值范围。
分析：先将原问题转化为不等式ax2-2x+2>0在 有解，再利用参数分离求解。
解答：(1)若 ， 在 内有有解
令 当 时，
所以a>-4,所以a的取值范围是
变式：若关于x的方程 有实根,求实数a的取值范围。
直线和圆位置关系
①直线和圆无公共点，称相离。 AB与圆O相离，d>r。
②直线和圆有两个公共点，称相交，这条直线叫做圆的割线。AB与O相交，d
③直线和圆有且只有一公共点，称相切，这条直线叫做圆的切线，这个唯一的公共点叫做切点。AB与O相切，d=r。(d为圆心到直线的距离)
平面内，直线Ax+By+C=0与圆x^2+y^2+Dx+Ey+F=0的位置关系判断一般方法是：
1.由Ax+By+C=0，可得y=(-C-Ax)/B，(其中B不等于0)，代入x^2+y^2+Dx+Ey+F=0，即成为一个关于x的方程
如果b^2-4ac>0，则圆与直线有2交点，即圆与直线相交。
如果b^2-4ac=0，则圆与直线有1交点，即圆与直线相切。
如果b^2-4ac<0，则圆与直线有0交点，即圆与直线相离。
2.如果B=0即直线为Ax+C=0，即x=-C/A，它平行于y轴(或垂直于x轴)，将x^2+y^2+Dx+Ey+F=0化为(x-a)^2+(y-b)^2=r^2。令y=b，求出此时的两个x值x1、x2，并且规定x1
当x=-C/Ax2时，直线与圆相离;
拓展阅读：
初中数学知识点总结：平面直角坐标系
平面直角坐标系
平面直角坐标系：在平面内画两条互相垂直、原点重合的数轴，组成平面直角坐标系。
水平的数轴称为x轴或横轴，竖直的数轴称为y轴或纵轴，两坐标轴的交点为平面直角坐标系的原点。
平面直角坐标系的要素：①在同一平面②两条数轴③互相垂直④原点重合
三个规定：
①正方向的规定横轴取向右为正方向，纵轴取向上为正方向
②单位长度的规定；一般情况，横轴、纵轴单位长度相同；实际有时也可不同，但同一数轴上必须相同。
③象限的规定：右上为第一象限、左上为第二象限、左下为第三象限、右下为第四象限。
相信上面对平面直角坐标系知识的讲解学习，同学们已经能很好的掌握了吧，希望同学们都能考试成功。
初中数学知识点：平面直角坐标系的构成
对于平面直角坐标系的构成内容，下面我们一起来学习哦。
平面直角坐标系的构成
（1）笔算两位数加法，要记三条
1、相同数位对齐；
2、从个位加起；
3、个位满10向十位进1。
（2）笔算两位数减法，要记三条
1、相同数位对齐；
2、从个位减起；
3、个位不够减从十位退1，在个位加10再减。
（3）混合运算计算法则
1、在没有括号的算式里，只有加减法或只有乘除法的，都要从左往右按顺序运算；
2、在没有括号的算式里，有乘除法和加减法的，要先算乘除再算加减；
3、算式里有括号的要先算括号里面的。
（4）四位数的读法
1、从高位起按顺序读，千位上是几读几千，百位上是几读几百，依次类推；
2、中间有一个0或两个0只读一个“零”；
3、末位不管有几个0都不读。
（5）四位数写法
1、从高位起，按照顺序写；
2、几千就在千位上写几，几百就在百位上写几，依次类推，中间或末尾哪一位上一个也没有，就在哪一位上写“0”。
（6）四位数减法也要注意三条
1、相同数位对齐；
2、从个位减起；
3、哪一位数不够减，从前位退1，在本位加10再减。
（7）一位数乘多位数乘法法则
1、从个位起，用一位数依次乘多位数中的每一位数；
2、哪一位上乘得的积满几十就向前进几。
（8）除数是一位数的除法法则
1、从被除数高位除起，每次用除数先试除被除数的前一位数，如果它比除数小再试除前两位数；
2、除数除到哪一位，就把商写在那一位上面；
3、每求出一位商，余下的数必须比除数小。
（9）一个因数是两位数的乘法法则
1、先用两位数个位上的数去乘另一个因数，得数的末位和两位数个位对齐；
2、再用两位数的十位上的数去乘另一个因数，得数的末位和两位数十位对齐；
3、然后把两次乘得的数加起来。
（10）除数是两位数的除法法则
1、从被除数高位起，先用除数试除被除数前两位，如果它比除数小，
2、除到被除数的哪一位就在哪一位上面写商；
3、每求出一位商，余下的数必须比除数小。
（11）万级数的读法法则
1。先读万级，再读个级；
2。万级的数要按个级的读法来读，再在后面加上一个“万”字；
3。每级末位不管有几个0都不读，其它数位有一个0或连续几个零都只读一个“零”。
（12）多位数的读法法则
1。从高位起，一级一级往下读；
2。读亿级或万级时，要按照个级数的读法来读，再往后面加上“亿”或“万”字；
3。每级末尾的0都不读，其它数位有一个0或连续几个0都只读一个零。
（13）小数大小的比较
比较两个小数的大小，先看它们整数部分，整数部分大的那个数就大，整数部分相同的，十分位上的数大的那个数就大，十分位数也相同的，百分位上的数大的那个数就大，依次类推。
（14）小数加减法计算法则
计算小数加减法，先把小数点对齐（也就是把相同的数位上的数对齐），再按照整数加减法则进行计算，最后在得数里对齐横线上的小数点位置，点上小数点。
（15）小数乘法的计算法则
计算小数乘法，先按照乘法的法则算出积，再看因数中一共几位小数，就从积的右边起数出几位，点上小数点。
（16）除数是整数除法的法则
除数是整数的小数除法，按照整数除法的法则去除，商的小数点要和被除数小数点对齐，如果除到被除数的末尾仍有余数，就在余数后面添0再继续除。
（17）除数是小数的除法运算法则
除数是小数的除法，先移动除数小数点，使它变成整数；除数的小数点向右移几位，被除数小数点也向右移几位（位数不够在被除数末尾用0补足）然后按照除数是整数的小数除法进行计算。
（18）解答应用题步骤
1。弄清题意，并找出已知条件和所求问题，分析题里的数量关系，确定先算什么，再算什么，最后算什么；
2。确定每一步该怎样算，列出算式，算出得数；
3。进行检验，写出答案。
（19）列方程解应用题的一般步骤
1。弄清题意，找出未知数，并用X表示；
2。找出应用题中数量之间的相等关系，列方程；
3。解方程；
4。检验、写出答案。
（20）同分母分数加减的法则
同分母分数相加减，分母不变，只把分子相加减。
（21）同分母带分数加减的法则
带分数相加减，先把整数部分和分数部分分别相加减，再把所得的数合并起来。
（22）异分母分数加减的法则
异分母分数相加减，先通分，然后按照同分母分数加减的法则进行计算。
（23）分数乘以整数的计算法则
分数乘以整数，用分数的分子和整数相乘的积作分子，分母不变。
（24）分数乘以分数的计算法则
分数乘以分数，用分子相乘的积作分子，分母相乘的积作分母。
（25）一个数除以分数的计算法则
一个数除以分数，等于这个数乘以除数的倒数。
（26）把小数化成百分数和把百分数化成小数的方法
把小数化成百分数，只要把小数点向右移动两位，同时在后面添上百分号；
把百分数化成小数，把百分号去掉，同时小数点向左移动两位。
（27）把分数化成百分数和把百分数化成分数的方法
把分数化成百分数，通常先把分数化成小数（除不尽通常保留三位小数），再把小数化成百分数；
把百分数化成小数，先把百分数改写成分母是100的分数，能约分的要约成最简分数。
二、小学数学口决定义归类
1。什么是图形的周长？
围成一个图形所有边长的总和就是这个图形的周长。
2。什么是面积？
物体的表面或围成的平面图形的大小叫做他们的面积。
3。加法各部分的关系：
一个加数=和-另一个加数
4。减法各部分的关系：
减数=被减数-差被减数=减数+差
5。乘法各部分之间的关系：
一个因数=积÷另一个因数
6。除法各部分之间的关系：
除数=被除数÷商被除数=商×除数
7。角
（1）什么是角？
从一点引出两条射线所组成的图形叫做角。
（2）什么是角的顶点？
围成角的端点叫顶点。
（3）什么是角的边？
围成角的射线叫角的边。
（4）什么是直角？
度数为90°的角是直角。
（5）什么是平角？
角的两条边成一条直线，这样的角叫平角。
（6）什么是锐角？
小于90°的角是锐角。
（7）什么是钝角？
大于90°而小于180°的角是钝角。
（8）什么是周角？
一条射线绕它的端点旋转一周所成的角叫周角，一个周角等于360°。
8。垂直问题
（1）什么是互相垂直？什么是垂线？什么是垂足？
两条直线相交成直角时，这两条线互相垂直，其中一条直线叫做另一条直线的垂线，这两条直线的交点叫做垂足。
（2）什么是点到直线的距离？
从直线外一点向一条直线引垂线，点和垂足之间的距离叫做这点到直线的距离。
9。三角形
（1）什么是三角形？
有三条线段围成的图形叫三角形。
（2）什么是三角形的边？
围成三角形的每条线段叫三角形的边。
（3）什么是三角形的顶点？
每两条线段的交点叫三角形的顶点。
（4）什么是锐角三角形？
三个角都是锐角的三角形叫锐角三角形。
（5）什么是直角三角形？
有一个角是直角的三角形叫直角三角形。
（6）什么是钝角三角形？
有一个角是钝角的三角形叫钝角三角形。
（7）什么是等腰三角形？
两条边相等的三角形叫等腰三角形。
（8）什么是等腰三角形的腰？
有等腰三角形里，相等的两个边叫做等腰三角形的腰。
（9）什么是等腰三角形的顶点？
两腰的交点叫做等腰三角形的顶点。
（10）什么是等腰三角形的底？
在等腰三角形中，与其它两边不相等的边叫做等腰三角形的底。
（11）什么是等腰三角形的底角？
底边上两个相等的角叫等腰三角形的底角。
（12）什么是等边三角形？
三条边都相等的三角形叫等边三角形，也叫正三角形。
（13）什么是三角形的高？什么叫三角形的底？
从三角形的一个顶点向它的对边引一条垂线，顶点和垂足之间的线段叫做三角形的高，这个顶点的对边叫三角形的底。
（14）三角形的内角和是多少度？
三角形内角和是180°。
10。四边形
（1）什么是四边形？
有四条线段围成的图形叫四边形。
（2）什么是平等四边形？
两组对边分别平行的四边形叫做平行四边形。
（3）什么是平行四边形的高？
从平行四边形一条边上的一点到对边引一条垂线，这个点和垂足之间的线段叫做四边形的高。
（4）什么是梯形？
只有一组对边平行的四边形叫做梯形。
（5）什么是梯形的底？
在梯形里互相平等的一组边叫梯形的底（通常较短的底叫上底，较长的底叫下底）。
（6）什么是梯形的腰？
在梯形里，不平等的一组对边叫梯形的腰。
（7）什么是梯形的高？
从上底的一点往下底引一条垂线，这个点和垂足之间的线段叫做梯形的高。
（8）什么是等腰梯形？
两腰相等的梯形叫做等腰梯形。
11。什么是自然数？
用来表示物体个数的0、1、2、3、4、5、6、7、8、9、10……是自然数（自然数都是整数）。
12。什么是四舍五入法？
求一个数的近似数时，看被省略的尾数位上的数是几，如果是4或者比4小，就把尾数舍去，如果是5或者比5大，去掉尾数后，要在它的前一位加1。这种求近似数的方法，叫做四舍五入法。
13。加法意义和运算定律
（1）什么是加法？
把两个数合并成一个数的运算叫加法。
（2）什么是加数？
相加的两个数叫加数。
（3）什么是和？
加数相加的结果叫和。
（4）什么是加法交换律？
两个数相加，交换加数的位置后，它的和不变，这叫做加法交换律。
14。什么是减法？
已知两个数的和与其中的一个加数，求另一个加数的运算叫做减法。
15。什么是被减数？什么是减数？什么叫差？
在减法中已知的和叫被减数，减去的已知数叫减数，所求的未知数叫差。
16。加法各部分间的关系：
和=加数+加数加数=和-另一加数
17。减法各部分间的关系：
差=被减数-减数减数=被减数-差被减数=减数+差
18。乘法
（1）什么是乘法？
求几个相同加数的和的简便运算叫乘法。
（2）什么是因数？
相乘的两个数叫因数。
（3）什么是积？
因数相乘所得的数叫积。
（4）什么是乘法交换律？
两个因数相乘，交换因数的位置，它们的积不变，这叫乘法交换律。
（5）什么是乘法结合律？
三个数相乘，先把前两个数相乘，再同第三个数相乘，或者先把后两个数相乘，再同第一个数相乘，它们的积不变，这叫乘法结合律。
19。除法
（1）什么是除法？
已知两个因数的积与其中的一个因数，求另一个因数的运算叫除法。
（2）什么是被除数？
在除法中，已知的积叫被除数。
（3）什么是除数？
在除法中，已知的一个因数叫除数。
（4）什么是商？
在除法中，求出的未知因数叫商。
20、乘法各部分的关系
积=因数×因数一个因数=积÷另一个因数
21。除法
（1）除法各部分间的关系：
商=被除数÷除数除数=被除数÷商
（2）有余数的除法各部分间的关系：
被除数=商×除数+余数
22。什么是名数？
通常量得的数和单位名称合起来的数叫名数。
23。什么是单名数？
只带有一个单位名称的数叫单名数。
24。什么是复名数？
有两个或两个以上单位名称的数叫复名数。
25。什么是小数？
仿照整数的写法，写在整数个位的右面，用圆点隔开，用来表示十分之几、百分之几、千分之几……的数叫小数。
26。什么是小数的基本性质？
小数的末尾添上零或者去掉零，小数大小不变，这叫小数的基本性质。
27。什么是有限小数？
小数部分的位数是有限的小数叫有限小数。
28。什么是无限小数？
小数部分的位数是无限的小数叫无限小数。
29。什么是循环节？
一个循环小数的部分依次不断重复出现的数叫做这个数的循环节。
30。什么是纯循环小数？
循环节从小数第一位开始的叫纯循环小数。
31。什么是混循环小数？
循环节不是从小数部分第一位开始的叫做混循环小数。
32。什么是四则运算？
我们把学过的加、减、乘、除四种运算统称四则运算。
33。什么是方程？
含有未知数的等式叫方程。
34。什么是解方程？
求方程解的过程叫解方程。
35。什么是倍数？什么叫约数？
如果a能被b整除，a就是b的倍数，b就叫a的约数（或a的因数）。
36。什么样的数能被2整除？
个位上是0、2、4、6、8的数都能被2整除。
37。什么是偶数？
能被2整除的数叫偶数。
38。什么是奇数？
不能被2整除的数叫奇数。
39。什么样的数能被5整除？
个位上是0或5的数能被5整除。
40。什么样的数能被3整除？
一个数的各位上的和能被3整除，这个数就能被3整除。
41。什么是质数（或素数）？
一个数如果只有1和它本身两个约数，这样的数叫质数。
42。什么是合数？
一个数除了1和它本身还有别的约数，这样的数叫合数。
43。什么是质因数？
每个合数都可以写成几个质数相乘的形式。其中每个质数都是这个合数的因数，叫做这个合数的质因数。
44。什么是分解质因数？
把一个合数用质因数相乘的形式表示出来叫做分解质因数。
45。什么是公约数？什么叫公约数？
几个数公有的约数叫公约数。其中的一个叫公约数。
46。什么是互质数？
公约数只有1的两个数叫互质数。
47。什么是公倍数？什么是最小公倍数？
几个数公有的倍数叫这几个数的公倍数。其中最小的一个叫这几个数的最小公倍数。
48。分数
（1）什么是分数？
把单位1平均分成若干份，表示这样的一份或者几份的数叫分数。
（2）什么是分数线？
在分数里中间的横线叫分数线。
（3）什么是分母？
分数线下面的部分叫分母。
（4）什么是分子？
分数线上面的部分叫分子。
（5）什么是分数单位？
把单位“1”平均分成若干份，表示其中的一份叫分数单位。
49、怎么比较分数大小？
（1）分母相同的两个分数，分子大的分数比较大。
（2）分子相同的两个分数，分母小的分子比较大。
（3）什么是真分数？
分子比分母小的分数叫真分数。
（4）什么是假分数？
分子比分母大或者分子和分母相等的分数叫假分数。
（5）什么是带分数？
由整分数和真分数合成的数通常叫带分数。
（6）什么是分数的基本性质？
分数的分子和分母同时乘或除以相同的数（0除外），分数大小不变，这就是分数的基本性质。
（7）什么是约分？
把一个分数化成同它相等，但分子、分母都比较小的数叫做约分。
（8）什么是最简分数？
分子、分母是互质数的分数叫最简分数。
50、比
（1）什么是比？
两个数相除又叫两个数的比。
（2）什么是比的前项？
比号前面的数叫比的前项。
（3）什么是比的后项？
比号后面的数叫比的后项。
（4）什么是比值？
比的前项除以后项所得的商叫比值。
（5）什么是比的基本性质？
比的前项和后项同时乘以或者同时除以相同的数（0除外）比值不变，这叫比的基本性质。
51。长方体和正方体
（1）什么是棱？
两个面相交的边叫棱。
（2）什么是顶点？
三条棱相交的点叫顶点。
（3）什么是长方体的长、宽、高？
相交于一个顶点的三条棱的长度分别叫长方体的长、宽、高。
（4）什么是正方体（立方体）？
长宽高都相等的长方体叫正方体（或立方体）。
（5）什么是长方体的表面积？
长方体六个面的总面积叫长方体的表面积。
（6）什么是物体体积？
物体所占空间的大小叫做物体的体积。
52、圆
（1）什么是圆心？
圆中心的点叫圆心。
（2）什么是半径？
连接圆心和圆上任意一点的线段叫半径。
（3）什么是直径？
通过圆心、并且两端都在圆上的线段叫直径。
（4）什么是圆的周长？
围成圆的曲线叫圆的周长。
（5）什么是圆周率？
我们把圆的周长和直径的比值叫圆周率。
（6）什么是圆的面积？
圆所围平面的大小叫圆的面积。
（7）什么是扇形？
一条弧和经过这条弧两端的两条半径所围成的图形叫扇形。
（8）什么是弧？
在圆上两点之间的部分叫弧。
（9）什么是圆心角？
顶点在圆心上的角叫圆心角。
（10）什么是对称图形？
如果一个图形沿着一条直线对折，两侧图形能够完全重合，这样的图形就是对称图形。
53、什么是百分数？
表示一个数是另一个数百分之几的数叫百分数，百分数也叫百分率或百分比。
54、比例
（1）什么是比例？
表示两个比相等的式子叫比例。
（2）什么是比例的项？
组成比例的四个数叫比例的项。
（3）什么是比例外项？
两端的两项叫比例外项。
（4）什么是比例内项？
中间的两项叫比例内项。
（5）什么是比例的基本性质？
在比例中两个外项的积等于两个内项的积。
（6）什么是解比例？
求比例中的未知项叫解比例。
（7）什么是正比例关系？
两种相关的量，一种变化，另一种量也变化，如果这两种量中相对应的两个数的比值（也就是商）一定，这两种量叫正比例的量，它们的关系叫正比例关系。
（8）什么是反比例关系？
两种相关的量，一种变化，另一种也随着变化，如果这两种量中相对应的积一定，这两种量叫反比例的量，它们的关系成反比例关系。
55、圆柱
（1）什么是圆柱底面？
圆柱的上下两个面叫圆柱的底面。
（2）什么是圆柱的侧面？
圆柱的曲面叫圆柱的侧面。
（3）什么是圆柱的高？
圆柱两个底面的距离叫圆柱的高。
三、小学数学量的计算单位及进率归类
1、长度计量单位及进率
千米（公里）、米、分米、厘米、毫米
1千米=1公里1千米=1000米
1米=10分米1分米=10厘米
1厘米=10毫米
2、面积计量单位及进率
平方千米、公顷、平方米、平方分米、平方厘米
1平方千米=100公顷
1平方千米=1000000平方米
1公顷=10000平方米
1平方米=100平方分米
1平方分米=100平方厘米
3、体积容积计量单位及进率
立方米、立方分米、立方厘米、升、毫升
1立方米=1000立方分米
1立方分米=1000立方厘米
1立方分米=1升1立方厘米=1毫升
4、质量单位及进率
吨、千克、公斤、克
1吨=1000千克
1千克=1公斤
1千克=1000克
5、时间单位及进率
世纪、年、月、日、小时、分、秒
1世纪=100年1年=12月
1天=24小时1小时=60分
1分=60秒
（31天的月份有1、3、5、7、8、10、12月份，30天的月份有4、6、9、11月份，平年2月28天，闰年2月29天）
四、常用计算公式表
1、长方形面积
=长×宽，计算公式S=ab
2、正方形面积
=边长×边长，计算公式S=a×a=a2
3、长方形周长
=（长+宽）×2，计算公式C=(a+b)×2
4、正方形周长
=边长×4，计算公式C=4a
5、平行四边形面积
=底×高，计算公式S=ah
6、三角形面积
=底×高÷2，计算公式S=a×h÷2
7、梯形面积
=（上底+下底）×高÷2，计算公式S=(a+b)×h÷2
8、长方体体积
=长×宽×高，计算公式V=abh
9、圆的面积
=圆周率×半径平方，计算公式V=πr2
10、正方体体积
=棱长×棱长×棱长，计算公式V=a3
11、长方体和正方体的体积
都可以写成底面积×高，计算公式V=sh
1．有向线段的定义
线段的端点A为始点，端点B为终点，这时线段AB具有射线AB的方向.像这样，具有方向的线段叫做有向线段.记作：.
2.有向线段的三要素：有向线段包含三个要素：始点、方向和长度.
3.向量的定义：(1)具有大小和方向的量叫做向量.向量有两个要素：大小和方向.
(2)向量的表示方法：①用两个大写的英文字母及前头表示，有向线段来表示向量时，也称其为向量.书写时，则用带箭头的小写字母，，，来表示.
4.向量的长度（模）：如果向量=，那么有向线段的长度表示向量的大小，叫做向量的长度(或模)，记作||.
5．相等向量：如果两个向量和的方向相同且长度相等，则称和相等，记作：=.
6．相反向量：与向量等长且方向相反的向量叫做的相反向量，记作：-.
7．向量平行（共线）：如果两个向量方向相同或相反，则称这两个向量平行，向量平行也称向量共线.向量平行于向量，记作//.规定： //.
8．零向量：长度等于零的向量叫做零向量，记作：.零向量的方向是不确定的，是任意的.由于零向量方向的特殊性，解答问题时，一定要看清题目中是零向量还是非零向量.
9．单位向量：长度等于1的向量叫做单位向量.
10．向量的加法运算：
(1)向量加法的三角形法则
11．向量的减法运算
12、两向量的和差的模与两向量模的和差之间的关系
对于任意两个向量，，都有|||-|||||+||.
13．数乘向量的定义：
实数和向量的乘积是一个向量，这种运算叫做数乘向量，记作.
向量()的长度与方向规定为：(1)||=|
(2)当0时，与方向相同;当0时，与方向相反.
(3)当=0时，当=时，=.
14．数乘向量的运算律：(1))= (结合律)
(2)(+) =+(第一分配律)(3)(+)=+.(第二分配律)
15．平行向量基本定理
如果向量，则//的充分必要条件是，存在唯一的实数，使得=.
如果与不共线，若m=n，则m=n=0.
16．非零向量的单位向量：非零向量的单位向量是指与同向的单位向量，通常记作.
=||，即==(，)
17．线段中点的向量表达式
点M是线段AB的中点，O是平面内任意一点，则=(+).
18．平面向量的直角坐标运算：如果=(a1，a2)，=(b1，b2)，则
+=(a1+b1，a2+b2);-=(a1-b1，a2-b2);=(a1，a2).
19．利用两点表示向量：如果A(x1，y1)，B(x2，y2)，则=(x2-x1，y2-y1).
20.两向量相等和平行的条件：若=(a1，a2)，=(b1，b2) ，则
=a1=b1且a2=b2.
//a1b2-a2b1=0.特别地，如果b10，b20，则// =.
21．向量的长度公式：若=(a1，a2)，则||=.
22．平面上两点间的距离公式：若A(x1，y1)，B(x2，y2)，则||=.
23．中点公式
若点A(x1，y1)，点B(x2，y2)，点M(x，y)是线段AB的中点，则x=，y= .
24．重心公式
在ABC中，若A(x1，y1)，B(x2，y2)，A(x3，y3)，，ABC的重心为G(x，y)，则
x=，y=
25．（1)两个向量夹角的取值范围是[0，p]，即0，p.
当=0时，与同向;当=p时，与反向
当= 时，与垂直，记作.
(3)向量的内积定义：=||||cos.
其中，||cos叫做向量在向量方向上的正射影的数量.规定=0.
(4)内积的几何意义
与的内积的几何意义是的模与在方向上的正射影的数量，或的模与在 方向上的正射影数量的乘积
当0，90时，0;=90时，
90时，0.
26．向量内积的运算律：
(1)交换率
(2)数乘结合律
(3)分配律
(4)不满足组合律
27．向量内积满足乘法公式
【关键词】 过敏性紫癜
【摘要】 目的 依据过敏性紫癜临床表现，重新探究其中医病因病机，明确风、热、湿、毒、瘀五端交融为其特点，病变脏腑责之于肺与大肠。验证具有疏风清热、祛湿解毒、凉血消斑化瘀功能的方药――愈风消斑汤临床疗效。方法 以愈风消斑汤为基本方，随证化裁，治疗过敏性紫癜78例，同时患者忌动物蛋白饮食2~3个月，保持每天排便2~3次。结果 显效64例（82.1%），有效14例（17.9%），皮肤紫癜消失快，并发腹、关节、肾病变者少。结论 愈风消斑汤配合饮食、大便管理，是治疗过敏性紫癜疗效确切的方法、药物。
【关键词】 过敏性紫癜；中医药疗法；疏风清热；祛湿解毒；凉血消斑
【Abstract】 Objective To access the clinic results of decoction of curing wind and eliminating purpura （DCWEP） for the treatment of allergic purpura,which was based on the concept that allergic purpura was caused by the combination of wind,heat,damp,toxin and stasis.Methods Seventy-eight cases of allergic purpura were treated by DCWEP.Certain herbs were added to if neccessary.In addition,patients were asked not intake animal protein for 2~3 months,excret twice or three times a day.Results Sixty-four cases （82.1%） were superior effective,14（17.9%） were effective.Purpura dissapperared quickly and compications in abdomen,joints and kidneys seldom occured.Conclusion DCWEP plus food control and excretion manegement is effective for allergic purpura.
【Key words】 allergic purpura;TCM therapy;curing wind and clearing heat;eliminating dampness and resolving toxin;cooling blood;eliminating purpura and removing stasis
过敏性紫癜，又称出血性毛细血管中毒症或许兰―亨诺紫癜，是一种毛细血管变态反应性出血性疾病。主要由于机体对某些过敏物质发生变态反应而引起毛细血管壁通透性和脆性增高，是一种较常见的免疫血管性疾病。临床表现除皮肤紫癜外，常有皮疹及血管神经性水肿、关节炎、腹痛及肾炎等症状。属于中医学中的“血证”、“肌衄”、“斑疹”、“葡萄疫”范畴。我院血液科在2000年1月~2003年11月用疏风清热、祛湿解毒、凉血消斑化瘀方药―愈风消斑汤为主，治疗过敏性紫癜78例，现总结如下。
1 临床资料
1.1 一般资料 78例均为住院患者，其中男41例（52.6%），女37例（47.4%），年龄最大58岁，最小7岁，中位年龄21岁，病程2天~1年不等；单纯型48例（61.5%），混合型30例（38.5%），其中肾型28例（35.9%），腹型12例（15.4%），关节型12例（15.4%），但腹型、关节型几乎全部有肾改变。
1.2 诊断标准 按《血液病诊断及疗效标准》（张之南主编）［1］执行。
1.3 方法
1.3.1 中药 愈风消斑汤组成：黄芩、牛蒡子、防风、当归、白鲜皮、地肤子、苍耳子、蝉蜕、土茯苓、丹皮、大青叶、仙鹤草、赤芍、丹参、大黄、甘草。腹痛加白芍、蒲黄、五灵脂；关节痛加木瓜、防己、秦艽；血尿加小蓟、白茅根、墨旱莲；蛋白尿加黄芪、益母草。
1.3.2 抗过敏、补钙 扑尔敏4mg，每日3次口服；钙尔奇D 1片，每日1次口服。
1.3.3 其他 伴肾改变者予以川芎嗪120mg，每日1次静滴；保肾康4粒，每日3次口服。若肾改变1个月以上，尿蛋白（++）以上，予雷公藤10~20mg，每日3次口服。若较重，为混合型紫癜，可予地塞米松5~10mg/d，静滴3~5天。有感染者用抗生素。常规肠道驱虫。
1.3.4 调护 （1）忌食动物蛋白及致敏食品、药品。（2）避免长时间站立、行走。肾改变患者尽量卧床休息。预防感冒。（3）保持大便通畅，每日排便2~3次。
1.4 治疗结果
1.4.1 疗效判定标准 按《血液病诊断及疗效标准》（张之南主编）［1］判定，并与上海瑞金医院治疗350例疗效进行比较［2］。
1.4.2 治疗效果 见表1。
表1 综合治疗78例与瑞金医院治疗350例疗效比较 例（略）
摘 要：随着教育的不断改革发展，教学方法也在跟着变革优化。且苏教版的教材相对于其他版本的教材，本身灵活度就要高，在教授学习的过程中对于学生的思维能力要求更高一些，所以在实际的教学方法应用中，教师也更需要注意教学方法的合理性。为了使教育模式更加适应教育改革的推进，教育方法也需要合理优化，实际教育中要多利用利于教学活动开展的方法，及时在实践中进行方法的优化改进，以用来促进教学成效的提升，帮助更多的学生合理学习。针对苏教版初中数学教学过程中教学方法的应用进行讨论探究，实际分析改革教育中教学方法的合理使用。
关键词：初中数学；教学方法；特点
一、苏教版初中数学教材的特点
首先，苏教版数学教材一个显著特点就是注重学生思维能力的运用，更能体现学生的素质，并且教材内容贴近于生活，学生在日常学习中能够找到学习中应用的素材，一些数学模型与数学问题就是取自生活。教材也着重于学生的探究性学习能力，由于数学本身就是一个逻辑性极强的学科，对于学生的空间想象能力以及逻辑分析能力都有很高的要求，苏教版初中数学对于学生在这些方面的要求更高，苏教版初中数学课本内容能极大地提高学生学习的综合能力，只有学生实践过后才会有对数学知识的感知能力，生活体验被与数学知识点紧密地关联起来，数学知识点中抽象的理论知识与实践相连接，这些条件使苏教版数学更有助于让学生通过自主学习提升自己的数学知识素养，获得进步。还有一点就是苏教版数学知识更加注重数学知识体系构建的完整性，数学知识被数学方法巧妙地结合在一起，增强知识的连贯性，迫使学生增强数学逻辑思维能力，让思想变得严密、富有条理，最终掌握自己学到的知识框架结构。所以，学生在学习苏教版初中数学知识时，要注意学习方法的灵活运用，巧妙的学习方法将促使学生数学能力获得提升，相反的，没有适当的学习方式，会使学生丧失对数学的学习兴趣。
二、学生对苏教版初中数学学习方法的规划
学习苏教版数学教材就要抓住苏教版数学知识的特点，它往往存在于生活实践中，通过生活问题的实践，就会得到一定的数学灵感，所以在学习苏教版初中数学知识时，学生首先要进行课前预习，在课前进行预习探究，通过学生实践与初中数学知识内容进行联系探究，就会发现数学内容中的一些端倪，最终通过数学知识的运用得到结果。接下来就是课堂中老师的主导点拨，学生在自我探究时往往把握不到知识特点，造成学习效率低下，往往还学不到真正的知识，所以在学习中学生要注意老师的分析
思路，掌握教师的逻辑分析过程，为下次自我探究学习作铺垫，只有这样的循序渐进，才能掌握苏教版初中数学的学习方法。最后就是对所学知识要及时作总结分析，以便积累知识点，学会总结。只要学生在进行自我探究式学习过程中善于探讨问题，获取问题，总结问题，学习初中数学知识就要容易很多，数学学习方法的灵活使用能极大地提高学生的学习效率，加深学生对数学知识的理解。
三、教师对苏教版初中数学教学方法的使用
教师是数学教学中关键的教学人物，所以，教学方法的使用取决于教师对知识的掌控力，正确的教学方法能够提高数学教学效率，也能让学生真正学习到数学学习方法，增强学生的自我学习能力。系统的笛Ы萄Х椒ù涌吻暗既肟始，教师要引导学生进行数学知识的提前探讨，将所要学习的知识通过生活的情境实例引出，让学生在学习数学知识前进行生活实践，触发学生对数学的感受，再让学生进行自主探讨，这样可以将所要涉及的复杂的逻辑思维题式进行化简，通过生活实例，使学生快速地掌握数学知识内容，也可以增强学生对数学的兴趣。其次，在教授过程中，教师要让学生积极采用小组学习的模式进行初中数学学习，由于苏教版初中数学具有极强的探讨性，所以，要加强学生探讨能力，利用小组学习的模式使学生在学习过程中可以及时讨论自己所掌握的知识，共同探讨其正确性，教师则在这一过程中进行引导性的提示，促进小组成果的展现。在探讨过程结束后，教师就可以进行数学知识点的详细讲解，通过发现学生掌握知识的不足，逐一进行讲解，这样就利用到创新课堂的模式，让学生变为课堂的主体，更能促进学生对数学知识的掌握，迫使学生进行思考、探讨、总结，锻炼学生学习数学知识的综合能力。教师则在这一部分中作为总的规划者，提前做好相关教学计划，探索数学教学方法，将学生更好地引导到学习数学的道路中，提升学生学习数学的能力。
综上所述，苏教版初中数学本身具有的学科特点，促使教师使用特殊的教学手段，学生使用相应的学习方法，只有真正利用好学习数学的方法，认真总结规划，对于逻辑性与生活情境实践极强的苏教版初中数学知识，也能够进行很好的掌握。教师要注意强化数学知识点的生活实践性，增强教学中教学方法的趣味高效性，就能使学生真正掌握学习数学的方法，最终提升学生的全面素质。
参考文献：
对于初中数学学习，归类总结是一项巨大的工程，其中需要各种教学思想的加入，数学思想是一个重要并且应该具备的思想。因此，教师首先要不断更新教学观念，从思想上不断提高对引导法重要性的认识，深入钻研教材，根据教学要求将引导方法融入备课环节，写出有效的数学知识学习的引导实例教案。数学知识的学习与实际生活的联系非常紧密，更应该结合生活展开教学，做好知识点的阶段性复习，归类总结，使学生在不断学习中掌握知识点的前后联系和整体学习。同时，复习课堂的开始与结束的延续同等重要，应使他们认识到生活处处是数学和数学学习的无限性。但是，往往理想和现实总有一些差别。
一、插入知识点归类总结，引导建立互动交流平台
授课教师可根据教材知识的内容，将知识在教案中转化成其他问题的形式，让学生融入一种与知识相关问题的情境中，在激发学生学习兴趣的基础上让学生对数学知识概念进行思考。同时，试着寻找适合的理解方式，将前后知识点的学习进行不断总结，或者在教学的时候插入之前的内容，进行小规模的复习，使学生对知识点的吸收更加全面和合理，让学生在复习式的教学情境中逐步提高知识总结和解决问题的能力。教学中并不是问题琐碎，而是与所学知识点相关问题的不断总结，突出重点，启发思考。在初中数学课堂教学中引导学生参与交流互动，不仅可以达到提高学生的求知欲，而且可以促进课堂的有序进行，提高课堂效率。
例如，在讲“函数”复习课时，可设置如下提问：“同学们，通过之前的学习，我们对函数有了一定认识，那么，对《一元二次方程》《一元一次方程》《二元一次方程》的应用与对比，针对性地提出不同的解题步骤问题，通过类比，讨论，提出大胆猜想。在这样的情形下，一方面_到了课前问题的引入能引导学生预习的目的，另一方面也培养了学生自主思考问题的学习能力。
二、混合式复习教学模式
教师在上课之前，应将所要讲的某章内容做一个条理性的总结提纲，或者说期中总结等。同时，做好几种教学方式混合使用的教案，注重课堂复习教学中的多元化引入环节。有的学生对生活实际问题、教学方式等感兴趣，可通过某名学生提出的问题作为知识点总结的导线，通过问题讨论的方式获得局部知识的理解和应用，使知识点更加容易接受。另外，教师需按照《复纲》需求进行有序地讲解，不能随意教学，以避免误导学生，从而使不同层次的学生都能接受和掌握并应用这些初中数学知识体系。同时，要发挥课后对课堂的延续作用，教学并不是独立的，而是相互联系的。针对课堂或者下一节复习课的内容进行设问，对于学生来讲，当作是探索性的问题，既可以总结当节课的内容，又可以启发学生产生积极备战下一阶段的知识点总结的兴趣，为学生能够自主复习创造条件，也实现阶段性复习的良好效果。
例如，在讲“几何”的复习时，对“中心对称图形”和“轴对称图形”两节进行综合解析，混合教学，要事先准备好上课需要的工具，希望学生们通过观察的形式在学到知识的同时，可以增加好奇心和求知欲。
三、学生为主导，逐步引入解题思想
教材的研读需要达到把握课本基础知识，而知识点的阶段性总结则需要良好的教学思想的引入，教师培养学生研读的基本技能，这就需要重视数学思想方法的应用，把教学思想的培养当作兴趣培养的前驱，将这些思想引入课堂，学生把握了这些思想对今后的数学学习和数学知识的应用将产生深刻的影响。从初中阶段就重视引入数学思想的教学方法，将为学生后续学习打下坚实的思想基础，尤其是在教学的复习阶段中，教学思想的引入能大大提高学生归类总结的能力，也为阶段性复习提升效率。这些思想主要有：转化思想、数形结合思想、方程思想、函数思想等。教学思想的引入不仅能激发学生学习的兴趣，还能给予学生适当的兴趣延续，使学生认识到教学思想对学习的重要性。
例如，以方程思想为例，在讲“一元二次方程”的时候，从问题的数量关系入手，根据学生的预习情况，将问题转化为不同的设问，适当设定未知数，结合定义和已知条件、隐含条件，建立已知量和未知量之间的数量关系，以方程式或方程组的形式表达出来，从而使问题得到解决的思想方法。
四、加强课堂讨论的开展
对于数学的理解，我们都能想到它的计算过程和准确性。而阶段性的复习则需要学生不断地讨论与思考，将学生总结能力的培养结合提纲式知识点挖掘教材，将教材与知识点的总结结合起来，这样更能将提纲式复习作为阶段性复习教学中的主线，教师可以采用同桌交流、小组合作等多种课堂教学组织形式，这些形式能为学生提供合作交流的空间。同时，教师还必须给学生的自主学习提供充足的时间，以此充分调动学生学习数学的积极性，有效培养学生的学习兴趣。
例如，教师应以倾听学生的想法为主，如在讲“圆”的知识点时，学生会想起生活中的不同物体，那么学生可能会对其具有的性质做初步的猜测，授课教师对其评价总结。与此同时，规律的传授并不是单一的，应引导他们举一反三，将此性质应用到其他物体或者物质。
五、总结
